Let ABCD be a parallelogram. The lengths of the side AD and the diagonal AC are 10 cm and 20 cm, respectively. If the angle \(∠ADC \) is equal to 30° then the area of the parallelogram, in sq. cm, is
\(\frac{25(\sqrt{3}+\sqrt{15})}{2}\)
\(25(\sqrt5+\sqrt{15})\)
\(\frac{25(\sqrt5+\sqrt{15})}{2}\)
\(25(\sqrt3+\sqrt{15})\)
The Correct Option is D
Solution and Explanation
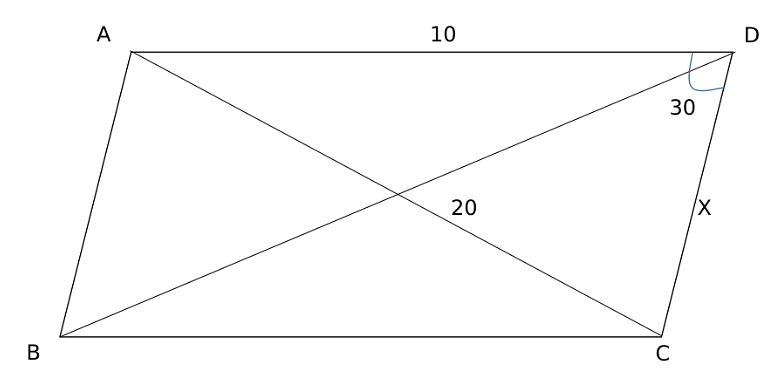
Applying the Cosine Rule in triangle ACD:
Using the cosine rule:
\( AC^2 = AD^2 + CD^2 - 2 \cdot AD \cdot CD \cdot \cos(∠ADC) \)
Given: \( AD = 10 \), \( CD = X \), \( ∠ADC = 30^\circ \), and \( AC = 20 \)
Substituting into the formula:
\( 100 + X^2 - 2 \cdot 10 \cdot X \cdot \cos(30^\circ) = 400 \)
Since \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \), we get:
\( X^2 - 10X\sqrt{3} - 300 = 0 \)
Solving the quadratic equation:
\( X = \frac{10\sqrt{3} \pm 10\sqrt{15}}{2} \)
Since \( X \) is the length of a side, it must be positive:
\( \Rightarrow X = \frac{10\sqrt{3} + 10\sqrt{15}}{2} \)
Finding the area of the parallelogram:
Area = base × height = \( 10 \cdot X \cdot \sin(30^\circ) \)
Since \( \sin(30^\circ) = \frac{1}{2} \), we get:
Area = \( 10 \cdot \frac{10\sqrt{3} + 10\sqrt{15}}{2} \cdot \frac{1}{2} \)
\( = \frac{10 \cdot (10\sqrt{3} + 10\sqrt{15})}{4} \)
\( = 25(\sqrt{3} + \sqrt{15}) \)
Final Answer: \( \boxed{25(\sqrt{3} + \sqrt{15})} \) square units
Top Questions on Geometry
- Surface area of a balloon (spherical), when air is blown into it, increases at a rate of 5 mm²/s. When the radius of the balloon is 8 mm, find the rate at which the volume of the balloon is increasing.
- The equation of chord AB of ellipse \(2x^2 + y^2 = 1\) is \(x - y + 1 = 0\). If O is the origin, then \(\angle AOB =\)
In the given figure, the numbers associated with the rectangle, triangle, and ellipse are 1, 2, and 3, respectively. Which one among the given options is the most appropriate combination of \( P \), \( Q \), and \( R \)?

- Let the sum of the focal distances of the point $ P(4, 3) $ on the hyperbola $ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $ be $ 8\sqrt{\frac{5}{3}} $. If for $ H $, the length of the latus rectum is $ \ell $ and the product of the focal distances of the point $ P $ is $ m $, then $ 9\ell^2 + 6m $ is equal to:
- Let for two distinct values of $ p $, the lines $ y = x + p $ touch the ellipse $ E: \frac{x^2}{4} + \frac{y^2}{9} = 1 $ at the points $ A $ and $ B $. Let the line $ y = x $ intersect $ E $ at the points $ C $ and $ D $. Then the area of the quadrilateral $ ABCD $ is equal to:
Questions Asked in CAT exam
- Bina incurs 19% loss when she sells a product at Rs. 4860 to Shyam, who in turn sells this product to Hari. If Bina would have sold this product to Shyam at the purchase price of Hari, she would have obtained 17% profit. Then, the profit, in rupees, made by Shyam is
- CAT - 2024
- Profit and Loss
- Gopi marks a price on a product in order to make 20% profit. Ravi gets 10% discount on this marked price, and thus saves Rs 15. Then, the profit, in rupees, made by Gopi by selling the product to Ravi, is
- CAT - 2024
- Profit and Loss
- The selling price of a product is fixed to ensure 40% profit. If the product had cost 40% less and had been sold for 5 rupees less, then the resulting profit would have been 50%. The original selling price, in rupees, of the product is
- CAT - 2024
- Profit and Loss
- A regular octagon ABCDEFGH has sides of length 6 cm each. Then the area, in sq. cm, of the square ACEG is
- CAT - 2024
- Mensuration
- The surface area of a closed rectangular box, which is inscribed in a sphere, is 846 sq cm, and the sum of the lengths of all its edges is 144 cm. The volume, in cubic cm, of the sphere is ?
- CAT - 2024
- Mensuration