Question

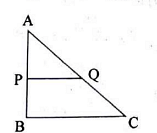
In the given figure, \(PQ||BC\). If AP=3 cm, BP=2 cm and CQ=3 cm, then AQ= 

• A. 4 cm
• B. 4.5 cm
• C. 3.5 cm
• D. 5 cm

Answer 1

The Correct Option is B

To solve the problem, we need to find the length of segment $AQ$ using the concept of similar triangles formed by a line parallel to one side of a triangle.

1. Understanding the Geometry:
In the given triangle, $PQ \parallel BC$, so triangles $APQ$ and $ABC$ are similar by Basic Proportionality Theorem (Thales' Theorem).

2. Given Information:
$AP = 3 \, \text{cm}$
$BP = 2 \, \text{cm}$
$CQ = 3 \, \text{cm}$

3. Use of Similar Triangles:
Since $PQ \parallel BC$, we write the similarity condition:

$ \frac{AP}{PB} = \frac{AQ}{QC} $

4. Substituting the Known Values:
$ \frac{3}{2} = \frac{AQ}{3} $

5. Cross Multiplying to Solve for $AQ$:
$ 3 \times 3 = 2 \times AQ $
$ 9 = 2AQ \Rightarrow AQ = \frac{9}{2} = 4.5 \, \text{cm} $

Final Answer:
The length of $AQ$ is $ 4.5 \, \text{cm} $.