In the circuit shown below, the switch $S$ is connected to position $P$ for a long time so that the charge on the capacitor becomes $q _{1}\, \mu C$ Then $S$ is switched to position $Q$ After a long time, the charge on the capacitor is $q _{2}\, \mu C$
The magnitude of $q_2$ is ____
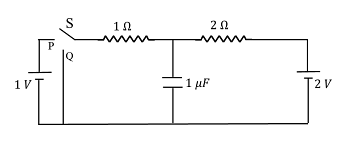
The magnitude of $q_2$ is ____
Correct Answer: 0.67
Solution and Explanation
Answer: 0.67
Top Questions on Current electricity
- Find the equivalent resistance between two ends of the following circuit:
- JEE Main - 2025
- Physics
- Current electricity
Given below are two statements. One is labelled as Assertion (A) and the other is labelled as Reason (R):
Assertion (A): In an insulated container, a gas is adiabatically shrunk to half of its initial volume. The temperature of the gas decreases.
Reason (R): Free expansion of an ideal gas is an irreversible and an adiabatic process.In the light of the above statements, choose the correct answer from the options given below:
- JEE Main - 2025
- Physics
- Current electricity
- Two conductors A and B of the same material have their lengths in the ratio 1:2 and radii in the ratio 2:3. If they are connected in parallel across a battery, the ratio \( \frac{v_A}{v_B} \) of the drift velocities of electrons in them will be:
- CBSE CLASS XII - 2025
- Physics
- Current electricity
- A conductor of length \( l \) is connected across an ideal cell of emf E. Keeping the cell connected, the length of the conductor is increased to \( 2l \) by gradually stretching it. If R and \( R' \) are initial and final values of resistance and \( v_d \) and \( v_d' \) are initial and final values of drift velocity, find the relation between:
\( R' \) and \( R \)
\( R' = 4R \)- CBSE CLASS XII - 2025
- Physics
- Current electricity
- \( n \) identical cells, each of e.m.f \( E \) and internal resistance \( r \), are connected in series. Later on, it was found that two cells ‘X’ and ‘Y’ are connected in reverse polarities. Calculate the potential difference across the cell ‘X’.
- CBSE CLASS XII - 2025
- Physics
- Current electricity
Questions Asked in JEE Advanced exam
- Let \(S=\left\{\begin{pmatrix} 0 & 1 & c \\ 1 & a & d\\ 1 & b & e \end{pmatrix}:a,b,c,d,e\in\left\{0,1\right\}\ \text{and} |A|\in \left\{-1,1\right\}\right\}\), where |A| denotes the determinant of A. Then the number of elements in S is _______.
- JEE Advanced - 2024
- Matrices
- A positive, singly ionized atom of mass number \( A_M \) is accelerated from rest by the voltage \( 192 \, \text{V} \). Thereafter, it enters a rectangular region of width \( w \) with magnetic field \( \vec{B}_0 = 0.1\hat{k} \, \text{T} \). The ion finally hits a detector at the distance \( x \) below its starting trajectory. Which of the following option(s) is(are) correct? \[ \text{(Given: Mass of neutron/proton = } \frac{5}{3} \times 10^{-27} \, \text{kg, charge of the electron = } 1.6 \times 10^{-19} \, \text{C).} \]
- JEE Advanced - 2024
- Electromagnetic Field (EMF)
- A thin stiff insulated metal wire is bent into a circular loop with its two ends extending tangentially from the same point of the loop. The wire loop has mass \( m \) and radius \( r \) and is in a uniform vertical magnetic field \( B_0 \). When a current \( I \) is passed through the loop, the loop turns about the line PQ by an angle \( \theta \). The angle \( \theta \) is given by:
- JEE Advanced - 2024
- Electromagnetic Field (EMF)
- A region in the form of an equilateral triangle (in x-y plane) of height \( L \) has a uniform magnetic field \( \mathbf{B} \) pointing in the \( +z \)-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height \( L \), is placed in the x-y plane with its vertex \( P \) at \( x = 0 \) in the orientation shown in the figure. At \( t = 0 \), the loop starts entering the region of the magnetic field with a uniform velocity \( \mathbf{v} \) along the \( +x \)-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
Which of the following graphs best depicts the variation of the induced emf (\( \mathcal{E} \)) in the loop as a function of the distance (\( x \)) starting from \( x = 0 \)?- JEE Advanced - 2024
- Radioactivity
- A table tennis ball has radius \( \frac{3}{2} \times 10^{-2} \, \text{m} \) and mass \( \frac{22}{7} \times 10^{-3} \, \text{kg} \). It is slowly pushed down into a swimming pool to a depth \( d = 0.7 \, \text{m} \) below the water surface and then released from rest. It emerges from the water surface at speed \( v \), without getting wet, and rises to a height \( H \). Which of the following option(s) is(are) correct?\(\text{(Given: } \pi = \frac{22}{7}, g = 10 \, \text{m/s}^2, \text{density of water} = 1 \times 10^3 \, \text{kg/m}^3, \text{viscosity of water} = 1 \times 10^{-3} \, \text{Pa.s).}\)
- JEE Advanced - 2024
- Radioactivity
Concepts Used:
Current Electricity
Current electricity is defined as the flow of electrons from one section of the circuit to another.
Types of Current Electricity
There are two types of current electricity as follows:
Direct Current
The current electricity whose direction remains the same is known as direct current. Direct current is defined by the constant flow of electrons from a region of high electron density to a region of low electron density. DC is used in many household appliances and applications that involve a battery.
Alternating Current
The current electricity that is bidirectional and keeps changing the direction of the charge flow is known as alternating current. The bi-directionality is caused by a sinusoidally varying current and voltage that reverses directions, creating a periodic back-and-forth motion for the current. The electrical outlets at our homes and industries are supplied with alternating current.