Question:
In an X-ray diffraction experiment with Cu crystals having lattice parameter \( 3.61 \, \text{Å} \), X-rays of wavelength of \( 0.090 \, \text{nm} \) are incident on the family of planes \( \{ 1 1 0 \} \). The highest order present in the diffraction pattern is .......
In an X-ray diffraction experiment with Cu crystals having lattice parameter \( 3.61 \, \text{Å} \), X-rays of wavelength of \( 0.090 \, \text{nm} \) are incident on the family of planes \( \{ 1 1 0 \} \). The highest order present in the diffraction pattern is .......
Show Hint
In X-ray diffraction, the highest diffraction order can be calculated using Bragg's law and the distance between the planes.
Updated On: Dec 6, 2025
Hide Solution
Verified By Collegedunia
Correct Answer: 5
Solution and Explanation
Step 1: Use the Bragg's law.
Bragg’s law for diffraction is given by \[ n \lambda = 2 d \sin \theta, \] where \( n \) is the diffraction order, \( \lambda \) is the wavelength, \( d \) is the distance between the planes, and \( \theta \) is the diffraction angle. Step 2: Calculate the distance between planes.
The lattice parameter \( a = 3.61 \, \text{Å} \) and for the \( \{ 1 1 0 \} \) planes, \[ d = \frac{a}{\sqrt{h^2 + k^2 + l^2}} = \frac{3.61}{\sqrt{1^2 + 1^2 + 0^2}} = \frac{3.61}{\sqrt{2}} = 2.55 \, \text{Å}. \] Step 3: Apply Bragg’s law for maximum diffraction order.
For the highest order diffraction, \( \theta = 90^\circ \), so \[ n = \frac{2 d}{\lambda}. \] Substitute the values \( d = 2.55 \, \text{Å} \) and \( \lambda = 0.090 \, \text{nm} = 0.090 \times 10^{-1} \, \text{Å} \): \[ n = \frac{2 \times 2.55}{0.090} \approx 56.67. \] Thus, the highest integer \( n \) is 56. Final Answer: The highest order present in the diffraction pattern is \( \boxed{56}. \)
Bragg’s law for diffraction is given by \[ n \lambda = 2 d \sin \theta, \] where \( n \) is the diffraction order, \( \lambda \) is the wavelength, \( d \) is the distance between the planes, and \( \theta \) is the diffraction angle. Step 2: Calculate the distance between planes.
The lattice parameter \( a = 3.61 \, \text{Å} \) and for the \( \{ 1 1 0 \} \) planes, \[ d = \frac{a}{\sqrt{h^2 + k^2 + l^2}} = \frac{3.61}{\sqrt{1^2 + 1^2 + 0^2}} = \frac{3.61}{\sqrt{2}} = 2.55 \, \text{Å}. \] Step 3: Apply Bragg’s law for maximum diffraction order.
For the highest order diffraction, \( \theta = 90^\circ \), so \[ n = \frac{2 d}{\lambda}. \] Substitute the values \( d = 2.55 \, \text{Å} \) and \( \lambda = 0.090 \, \text{nm} = 0.090 \times 10^{-1} \, \text{Å} \): \[ n = \frac{2 \times 2.55}{0.090} \approx 56.67. \] Thus, the highest integer \( n \) is 56. Final Answer: The highest order present in the diffraction pattern is \( \boxed{56}. \)
Was this answer helpful?
0
0
Top Questions on X Rays and the Ordering of the Elements
- The shortest wavelength, present in X-rays produced by an accelerating potential of 50kV, is:
- CUET (PG) - 2025
- Material Science and Technology
- X Rays and the Ordering of the Elements
- In Laue's technique of X-ray diffraction, a single crystal is held stationary and the beam of white radiation of wavelength \(\lambda\) is inclined at which condition with glancing angle (\(\theta\)):
- CUET (PG) - 2025
- Material Science and Technology
- X Rays and the Ordering of the Elements
- The minimum wavelength of X-rays produced by 20 keV electrons is nearly
- AP EAPCET - 2025
- Physics
- X Rays and the Ordering of the Elements
- An X-ray beam of initial intensity I0 of 70 keV imaging the chest is assumed to undergo attenuation through the muscle tissue for a thickness of 16 cm and further through the bone tissue for a thickness of 4 cm. The half value layer (HVL) thicknesses for the muscle and bone are 3.5 cm and 1.8 cm, respectively. The percentage of X-ray intensity transmitted through the body is ________.
Give your answer rounded off to 2 decimal places.- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
- The X-ray attenuation coefficients as a function of photon energy for three materials are shown in the figure below. A tissue phantom containing these three materials is imaged at two different X-ray photon energies of 50 keV and 150 keV. When the developed X-ray film is viewed, which of the following statements is/are TRUE ?
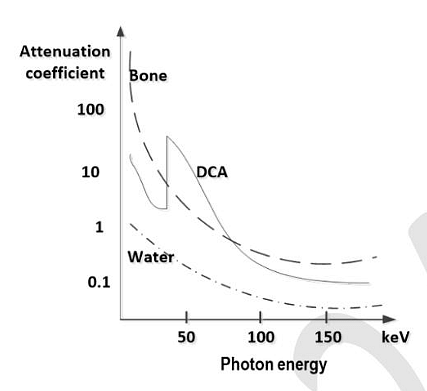
- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
View More Questions
Questions Asked in IIT JAM exam
- Consider a volume V enclosed by a closed surface S having unit surface normal \(\hat{n}\). For \(\mathbf{r} = x\hat{i} + y\hat{j} + z\hat{k}\), the value of the surface integral \(\frac{1}{9} \oint_{S} \mathbf{r} \cdot \hat{n} \,dS\) is
- IIT JAM PH - 2025
- Vector Calculus
- For a Zener diode as shown in the circuit diagram below, the Zener voltage \(V_Z\) is 3.7 V. For a load resistance (\(R_L\)) of 1 k\(\Omega\), a current \(I_1\) flows through the load. If \(R_L\) is decreased to 500 \(\Omega\), the current changes to \(I_2\). The ratio \(\frac{I_2}{I_1}\) is \rule{1cm{0.15mm}. (up to two decimal places)}

- IIT JAM PH - 2025
- Analog Electronics
- The shortest distance between an object and its real image formed by a thin convex lens of focal length 20 cm is _____ cm. (in integer)
- If \(\left(\frac{1-i}{1+i}\right)^{n/2} = -1\), where \(i = \sqrt{-1}\), one possible value of n is
- IIT JAM PH - 2025
- Complex numbers
- In a two-level atomic system, the excited state is 0.2 eV above the ground state. Considering the Maxwell-Boltzmann distribution, the temperature at which 2% of the atoms will be in the excited state is _____ K. (up to two decimal places)
(Boltzmann constant \(k_B = 8.62 \times 10^{-5}\) eV/K)
- IIT JAM PH - 2025
- Mechanics
View More Questions