In a one-litre flask, 6 moles of A undergoes the reaction A (g) ⇌ P (g). The progress of product formation at two temperatures (in Kelvin), T1 and T2, is shown in the figure:
If T1 = 2T2 and (∆G2Θ − ∆G1Θ) = RT2 ln x, then the value of x is ___ .
[∆G1Θ and ∆G2Θ are standard Gibb’s free energy change for the reaction at temperatures T1 and T2, respectively.]
If T1 = 2T2 and (∆G2Θ − ∆G1Θ) = RT2 ln x, then the value of x is ___ .
[∆G1Θ and ∆G2Θ are standard Gibb’s free energy change for the reaction at temperatures T1 and T2, respectively.]
Correct Answer: 8
Solution and Explanation
The answer is 8.
Top Questions on Law Of Chemical Equilibrium And Equilibrium Constant
- For the reaction in equilibrium:
N2(g) + 3H2(g) ⇌ 2NH3(g), ΔH = -Q
Reaction is favoured in forward direction by:- NEET (UG) - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- At a given temperature and pressure, the equilibrium constant values for the equilibria are given below:
\[ 3A_2 + B_2 \rightleftharpoons 2A_3B, \, K_1 \]
\[ A_3B \rightleftharpoons \frac{3}{2}A_2 + \frac{1}{2}B_2, \, K_2 \]
The relation between \( K_1 \) and \( K_2 \) is:- NEET (UG) - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- At \(-20^\circ \text{C}\) and 1 atm pressure, a cylinder is filled with an equal number of \(H_2\), \(I_2\), and \(HI\) molecules for the reaction:
\[H_2(g) + I_2(g) \rightleftharpoons 2HI(g)\] The \(K_P\) for the process is \(x \times 10^{-1}\).
\(x = ___________)
Given: \(R = 0.082 \, \text{L atm K}^{-1} \text{mol}^{-1}\)- JEE Main - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- The equilibrium $\mathrm{Cr_2O_7^{2-}} \rightleftharpoons 2\mathrm{CrO_4^{2-}}$ is shifted to the right in:
- JEE Main - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- For the given hypothetical reactions, the equilibrium constants are as follows:
\[ X \rightleftharpoons Y; \, K_1 = 1.0 \]
\[ Y \rightleftharpoons Z; \, K_2 = 2.0 \]
\[ Z \rightleftharpoons W; \, K_3 = 4.0 \]
The equilibrium constant for the reaction
\[ X \rightleftharpoons W\]
is:- JEE Main - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
Questions Asked in JEE Advanced exam
- Consider the ellipse \(\frac{x^2}{9}+\frac{y^2}{4}=1\). Let S (p, q) be a point in the first quadrant such that \(\frac{p^2}{9}+\frac{q^2}{4}>1\). Two tangents are drawn from S to the ellipse, of which one meets the ellipse at one end point of the minor axis and the other meets the ellipse at a point T in the fourth quadrant. Let R be the vertex of the ellipse with positive x-coordinate and Obe the center of the ellipse. If the area of the triangle △ORT is \(\frac{3}{2}\) , then which of the following options is correct ?
- JEE Advanced - 2024
- Conic sections
- Among V(CO)6, Cr(CO)5, Cu(CO)3, Mn(CO)5, Fe(CO)5, [Co(CO)3]3-, [Cr(CO)4]4-, and Ir(CO)3, the total number of species isoelectronic with Ni(CO)4 is _________.
[Given, atomic number: V = 23, Cr=24, Mn 25, Fe 26, Co 27, Ni 28, Cu = 29, Ir = 77]- JEE Advanced - 2024
- Isomerism in Coordination Compounds
- Let \(\overrightarrow{OP}=\frac{\alpha-1}{\alpha}\hat{i}+\hat{j}+\hat{k},\overrightarrow{OQ}=\hat{i}+\frac{\beta-1}{\beta}\hat{j}+\hat{k}\) and \(\overrightarrow{OR}=\hat{i}+\hat{j}+\frac{1}{2}\hat{k}\) be three vector where α, β ∈ R - {0} and 0 denotes the origin. If \((\overrightarrow{OP}\times\overrightarrow{OQ}).\overrightarrow{OR}=0\) and the point (α, β, 2) lies on the plane 3x + 3y - z + l = 0, then the value of l is _______.
- JEE Advanced - 2024
- Vector Algebra
- A closed vessel contains 10 g of an ideal gas X at 300 K, which exerts 2 atm pressure. At the same temperature, 80 g of another ideal gas Y is added to it and the pressure becomes 6 atm. The ratio of root mean square velocities of X and Y at 300 K is
- JEE Advanced - 2024
- States of matter
- Let the function \(f:[1,\infin)→\R\) be defined by
\(f(t) = \begin{cases} (-1)^{n+1}2, & \text{if } t=2n-1,n\in\N, \\ \frac{(2n+1-t)}{2}f(2n-1)+\frac{(t-(2n-1))}{2}f(2n+1) & \text{if } 2n-1<t<2n+1,n\in\N. \end{cases}\)
Define \(g(x)=\int\limits_{1}^{x}f(t)dt,x\in(1,\infin).\) Let α denote the number of solutions of the equation g(x) = 0 in the interval (1, 8] and \(β=\lim\limits_{x→1+}\frac{g(x)}{x-1}\). Then the value of α + β is equal to _____.- JEE Advanced - 2024
- Integral Calculus
Concepts Used:
Law of Chemical Equilibrium
Law of Chemical Equilibrium states that at a constant temperature, the rate of a chemical reaction is directly proportional to the product of the molar concentrations of the reactants each raised to a power equal to the corresponding stoichiometric coefficients as represented by the balanced chemical equation.
Let us consider a general reversible reaction;
A+B ↔ C+D
After some time, there is a reduction in reactants A and B and an accumulation of the products C and D. As a result, the rate of the forward reaction decreases and that of backward reaction increases.
Eventually, the two reactions occur at the same rate and a state of equilibrium is attained.
By applying the Law of Mass Action;
The rate of forward reaction;
Rf = Kf [A]a [B]b
The rate of backward reaction;
Rb = Kb [C]c [D]d
Where,
[A], [B], [C] and [D] are the concentrations of A, B, C and D at equilibrium respectively.
a, b, c, and d are the stoichiometric coefficients of A, B, C and D respectively.
Kf and Kb are the rate constants of forward and backward reactions.
However, at equilibrium,
Rate of forward reaction = Rate of backward reaction.
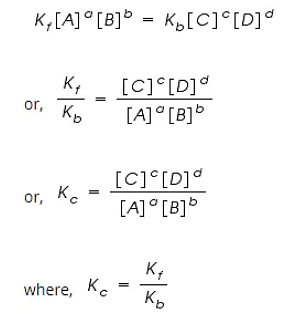
Kc is called the equilibrium constant expressed in terms of molar concentrations.
The above equation is known as the equation of Law of Chemical Equilibrium.