Question:
In a metal-deficient oxide sample, \(M_xY_2O_4\) (\(M\) and \(Y\) are metals), \(M\) is present in both \(+2\) and \(+3\) oxidation states and \(Y\) is in \(+3\) oxidation state. If the fraction of \(M^{2+}\) ions present in \(M\) is \(\frac{1}{3}\), the value of \(X\) is \_\_\_\_.
In a metal-deficient oxide sample, \(M_xY_2O_4\) (\(M\) and \(Y\) are metals), \(M\) is present in both \(+2\) and \(+3\) oxidation states and \(Y\) is in \(+3\) oxidation state. If the fraction of \(M^{2+}\) ions present in \(M\) is \(\frac{1}{3}\), the value of \(X\) is \_\_\_\_.
Show Hint
In metal-deficient oxides, balance the charges of all ions using the oxidation states and stoichiometry.
Updated On: Jan 20, 2025
- \(0.25\)
- \(0.33\)
- \(0.67\)
- \(0.75\)
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
Let \(M_xY_2O_4\) contain \(M^{2+}\) ions in a fraction of \(\frac{1}{3}\).
So, \(M^{2+} = \frac{x}{3}\) and \(M^{3+} = \frac{2x}{3}\). From charge neutrality: \[ \frac{2x}{3} \cdot (+3) + \frac{x}{3} \cdot (+2) + 2(+3) + 4(-2) = 0. \] Simplify: \begin{align*} \frac{2x}{3} + 2x - 2 &= 0
\frac{8x}{3} &= 2
x &= \frac{6}{8} = \frac{3}{4} = 0.75 \end{align*} Thus, the value of \(X\) is \(0.75\).
So, \(M^{2+} = \frac{x}{3}\) and \(M^{3+} = \frac{2x}{3}\). From charge neutrality: \[ \frac{2x}{3} \cdot (+3) + \frac{x}{3} \cdot (+2) + 2(+3) + 4(-2) = 0. \] Simplify: \begin{align*} \frac{2x}{3} + 2x - 2 &= 0
\frac{8x}{3} &= 2
x &= \frac{6}{8} = \frac{3}{4} = 0.75 \end{align*} Thus, the value of \(X\) is \(0.75\).
Was this answer helpful?
0
0
Top Questions on Metals and Non-Metals
- The number of valence electrons present in the metal among Cr, Co, Fe, and Ni which has the lowest enthalpy of atomisation is
- JEE Main - 2025
- Chemistry
- Metals and Non-Metals
- The first transition series metal 'M' has the highest enthalpy of atomisation in its series. One of its aquated ion (M$^{n+}$) exists in green colour. The nature of the oxide formed by the above M$^{n-}$ ion is:
- JEE Main - 2025
- Chemistry
- Metals and Non-Metals
- Which of the following ions shows spin only magnetic moment of 4.9 B.M.?
- JEE Main - 2025
- Chemistry
- Metals and Non-Metals
- The liquid metal is:
- Bihar BEd CET - 2024
- General Awareness
- Metals and Non-Metals
- The metal that occurs in the free form (native) is
- TS POLYCET - 2024
- Chemistry
- Metals and Non-Metals
View More Questions
Questions Asked in JEE Advanced exam
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
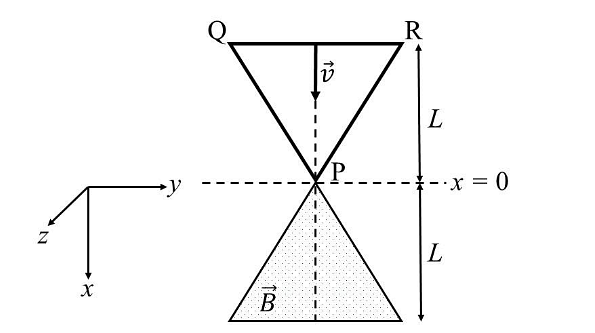
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - A positive, singly ionized atom of mass number \(A_M\) is accelerated from rest by the voltage \(192 V\). Thereafter, it enters a rectangular region of width 𝑤 with magnetic field \(\bar{B_0} = 0.1𝑘̂\)Tesla, as shown in the figure. The ion finally hits a detector at the distance 𝑥 below its starting trajectory. [Given: Mass of neutron/proton =\((5/3) × 10^{−27}\) kg, charge of the electron \(= 1.6 × 10^{−19} C.\)]

Which of the following option(s) is(are) correct?- JEE Advanced - 2024
- Electromagnetic waves
- Among the following, the correct statement(s) for electrons in an atom is(are)
- JEE Advanced - 2024
- Structure of atom
- An organic compound \(P\) with molecular formula \(C_6H_6O_3\) gives a ferric chloride test and does not have an intramolecular hydrogen bond. The compound \(P\) reacts with 3 equivalents of \(NH_2OH\) to produce oxime \(Q\). Treatment of \(P\) with excess methyl iodide in the presence of \(KOH\) produces compound \(R\) as the major product. Reaction of \(R\) with excess iso-butylmagnesium bromide followed by treatment with \(H_3O^+\) gives compound \(S\) as the major product. The total number of methyl (\(-CH_3\)) groups in compound \(S\) is \_\_\_\_\_.
- JEE Advanced - 2024
- Qualitative Analysis
- An organic compound P having molecular formula C6H6O3 gives ferric chloride test and does not have intramolecular hydrogen bond. The compound P reacts with 3 equivalents of NH2OH to produce oxime Q. Treatment of P with excess methyl iodide in the presence of KOH produces compound R as the major product. Reaction of R with excess iso-butylmagnesium bromide followed by treatment with H3O+ gives compound S as the major product.
The total number of methyl (−CH3) group(s) in compound S is ____.- JEE Advanced - 2024
- Aldehydes, Ketones and Carboxylic Acids
View More Questions