Question:
If U = { 1, 2, 3, 4, 5, 6, 7, 8 } is the universal set, A = { 2, 3, 6, 7 }, B = { 3, 4, 5, 6 }, and C = { 5, 6, 7, 8 }, then n[̅A ∩ (C - B)] + n[̅A ∩ (B ∨ C)] = k, where ̅A is the complement of set A. The value of k is:
If U = { 1, 2, 3, 4, 5, 6, 7, 8 } is the universal set, A = { 2, 3, 6, 7 }, B = { 3, 4, 5, 6 }, and C = { 5, 6, 7, 8 }, then n[̅A ∩ (C - B)] + n[̅A ∩ (B ∨ C)] = k, where ̅A is the complement of set A. The value of k is:
Show Hint
When working with set operations, remember to first calculate the union and difference, and then evaluate the intersection.
Updated On: Apr 17, 2025
- 2
- 3
- 4
- 7
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
We are given the universal set \( U \), and the sets \( A \), \( B \), and \( C \). First, we need to evaluate the two expressions:
1. \( A \cap (C - B) \): \( C - B = \{ 5, 6, 7, 8 \} - \{ 3, 4, 5, 6 \} = \{ 7, 8 \} \) So, \( A \cap (C - B) = \{ 2, 3, 6, 7 \} \cap \{ 7, 8 \} = \{ 7 \} \), and \( n[A \cap (C - B)] = 1 \).
2. \( A \cap (B \cup C) \): \( B \cup C = \{ 3, 4, 5, 6 \} \cup \{ 5, 6, 7, 8 \} = \{ 3, 4, 5, 6, 7, 8 \} \) So, \( A \cap (B \cup C) = \{ 2, 3, 6, 7 \} \cap \{ 3, 4, 5, 6, 7, 8 \} = \{ 3, 6, 7 \} \), and \( n[A \cap (B \cup C)] = 3 \).
Thus, \( k = 1 + 3 = 4 \).
1. \( A \cap (C - B) \): \( C - B = \{ 5, 6, 7, 8 \} - \{ 3, 4, 5, 6 \} = \{ 7, 8 \} \) So, \( A \cap (C - B) = \{ 2, 3, 6, 7 \} \cap \{ 7, 8 \} = \{ 7 \} \), and \( n[A \cap (C - B)] = 1 \).
2. \( A \cap (B \cup C) \): \( B \cup C = \{ 3, 4, 5, 6 \} \cup \{ 5, 6, 7, 8 \} = \{ 3, 4, 5, 6, 7, 8 \} \) So, \( A \cap (B \cup C) = \{ 2, 3, 6, 7 \} \cap \{ 3, 4, 5, 6, 7, 8 \} = \{ 3, 6, 7 \} \), and \( n[A \cap (B \cup C)] = 3 \).
Thus, \( k = 1 + 3 = 4 \).
Was this answer helpful?
0
0
Top Questions on Sets
- Mode of the data \( 19, 2, 6, 12, 12, 3, 5, 6, 18, 14, 6, 17, 2 \) is:
- The mean and mode of 5, 3, 9, 1, 9, 8, 9, 4 are m and n respectively, the value of m+n is?
- If A = {1, 2, {3, 4}, 5}, then which of the following is incorrect?
- If A and B are the two sets containing 3 and 6 elements respectively, then what can be the maximum number of elements in A∪B?
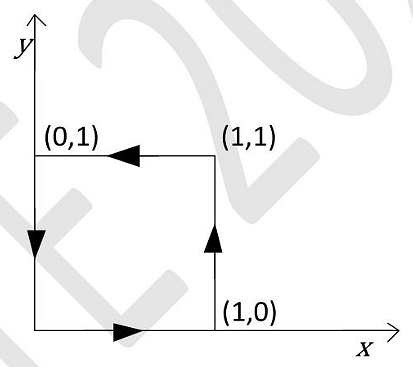
- For \(\vec{F}=(x+y)\hat{i}+(x+y)\hat{j}\) the value of \(\oint\vec{F}.d\vec{r}\) along the path shown in the figure is ________. Give your answer as an integer.
View More Questions
Questions Asked in NPAT exam
- Based on the given image, which of the following options must be true?

- NPAT - 2025
- Visual Reasoning
- A can draw 10 illustrations in 5 days. B is three times as productive in twice the amount of time (in comparison to A). How many illustrations can B draw in a day?
- NPAT - 2025
- Time and Work
- A, B and C have some marbles. The ratio of the number of marbles with A to the number with B is 2:1. Also, the number of marbles with A to the number with C is 1:4. What is the approximate percentage of the total number of marbles that are with C?
- NPAT - 2025
- Percentages
- If \( p \) and \( q \) are numbers such that the pair of linear equations \( (p + 2)x + (q - 1)y = 10 \) and \( (q + 2)x + (p - 1)y = 10 \) have infinite solutions for \( x \) and \( y \), then \( p = q \).
- NPAT - 2025
- Linear Equations
- If \( x \), \( y \), and \( z \) are positive integers and \( p = \left( \left( (x - 1)^2 / |x| \right) + 2 \right) + \left( \left( (y - 1)^2 / |y| \right) + 2 \right) + \left( \left( (z - 1)^2 / |z| \right) + 2 \right), \) then \( p<6 \).
- NPAT - 2025
- Algebra
View More Questions