If the net flux through a cube is 1.05 N m\(^2\) C\(^{-1}\), what will be the total charge inside the cube? (Given: The permittivity of free space is \(8.85 \times 10^{-12}\) C\(^2\) N\(^{-1}\) m\(^{-2}\)).
Show Hint
- \(9.29 \times 10^{-11}\) C
- \(9.27 \times 10^{-10}\) C
- \(9.22 \times 10^{-6}\) C
- \(9.29 \times 10^{-12}\) C
The Correct Option is D
Solution and Explanation
Step 1: Understanding the Concept:
This problem is a direct application of Gauss's Law of electrostatics. Gauss's Law states that the total electric flux (\(\Phi\)) through any closed surface is equal to the total net electric charge (\(Q_{\text{in}}\)) enclosed within that surface, divided by the permittivity of free space (\(\epsilon_0\)).
Step 2: Key Formula or Approach:
According to Gauss's Law:
\[ \Phi = \frac{Q_{\text{in}}}{\epsilon_0} \]
To find the total charge inside the cube, we can rearrange the formula:
\[ Q_{\text{in}} = \Phi \times \epsilon_0 \]
Step 3: Detailed Explanation:
Given:
Net electric flux, \( \Phi = 1.05 \, \text{N m}^2 \text{C}^{-1} \)
Permittivity of free space, \( \epsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2 \text{N}^{-1} \text{m}^{-2} \)
Now, we calculate the total charge enclosed, \(Q_{\text{in}}\):
\[ Q_{\text{in}} = (1.05 \, \text{N m}^2 \text{C}^{-1}) \times (8.85 \times 10^{-12} \, \text{C}^2 \text{N}^{-1} \text{m}^{-2}) \]
\[ Q_{\text{in}} = 9.2925 \times 10^{-12} \, \text{C} \]
Rounding to two decimal places, we get:
\[ Q_{\text{in}} \approx 9.29 \times 10^{-12} \, \text{C} \]
Step 4: Final Answer:
The total charge inside the cube will be \(9.29 \times 10^{-12}\) C.
Top Questions on Gauss Law
- An electric field \( \vec{E} = (2x \hat{i}) \, \text{N C}^{-1} \) exists in space. A cube of side \( 2 \, \text{m} \) is placed in the space as per the figure given below. The electric flux through the cube is __________ \( \text{N m}^2/\text{C} \).
- JEE Main - 2024
- Physics
- Gauss Law
- A charge q is placed at the center of one of the surface of a cube. The flux linked with the cube is :-
- JEE Main - 2024
- Physics
- Gauss Law
- There are two cubical Gaussian surface carrying charges as shown. Find ratio of fluxes through surface \(C_1\) and \(C_2\):

- JEE Main - 2024
- Physics
- Gauss Law
- Match List I with List IIChoose the correct answer from the options given below:
LIST I LIST II A Gauss's Law in Electrostatics I \(\oint \vec{E} \cdot d \vec{l}=-\frac{d \phi_B}{d t}\) B Faraday's Law II \(\oint \vec{B} \cdot d \vec{A}=0\) C Gauss's Law in Magnetism III \(\oint \vec{B} \cdot d \vec{l}=\mu_0 i_c+\mu_0 \in_0 \frac{d \phi_E}{d t}\) D Ampere-Maxwell Law IV \(\oint \vec{E} \cdot d \vec{s}=\frac{q}{\epsilon_0}\) - JEE Main - 2023
- Physics
- Gauss Law
- A cubical Gaussian surface has side of length a = 10 cm. Electric field lines are parallel to x-axis as shown. The magnitudes of electric fields through surfaces ABCD and EFGH are 6kNC-1 and 9kNC-1 respectively. Then the total charge enclosed by the cube is
[Take ε0 = 9 × 10-12 Fm-1]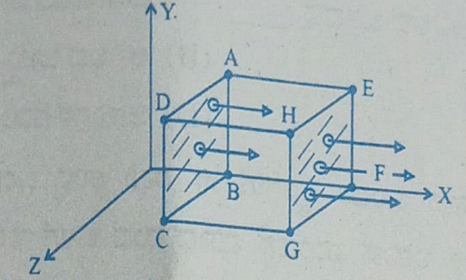
- KCET - 2023
- Physics
- Gauss Law
Questions Asked in CUET exam
- Rearrange the parts to form a logical sentence:
A) the city's new policy
B) has significantly improved
C) air quality
D) over the past year- CUET (UG) - 2025
- Sentence Arrangement
- Identify the option where the underlined phrase is used incorrectly: "She is interested on learning new languages."
- CUET (UG) - 2025
- Prepositions
- Which among the following does not belong to the fallacy of relevance?
- CUET (UG) - 2025
- Logical Reasoning
- Fill in the blank with the correct option:
She has been working here ___ five years.- CUET (UG) - 2025
- Prepositions
- In order to make a truth table for the following statement: \[ P \cdot (Q \vee R) \supset (P \equiv Q) \] if each truth functional connective is represented by the following letters, what would be the correct order of the columns in solving the truth table?
A. \(\cdot\)
B. \(\vee\)
C. \(\supset\)
D. \(\equiv\)
Choose the correct answer from the options given below:- CUET (UG) - 2025
- Logical Reasoning