If A'= \(\begin{bmatrix} 3 & 4 \\ -1 & 2 \\ 0 &1 \end{bmatrix}\)\(\begin{bmatrix} -1 & 2 & 1 \\ 1 &2 & 3\end{bmatrix}\) , then verify that
(i) \((A+B)'=A'+B' \)
(ii) \((A-B)'=A'-B'\)
(i) \((A+B)'=A'+B' \)
(ii) \((A-B)'=A'-B'\)
Solution and Explanation
(i) It is known that A=(A')'
Therefore, we have:
A= \(\begin{bmatrix} 3 & -1 & 0 \\ 4 & 2 & 1 \end{bmatrix}\)
B'= \(\begin{bmatrix} -1 & 1 \\ 2 & 2 \\ 1 &3 \end{bmatrix}\)
\(A+B\) = \(\begin{bmatrix} 3 & -1 & 0 \\ 4 & 2 & 1 \end{bmatrix}\) + \(\begin{bmatrix} -1 & 2 & 1 \\ 1 &2 & 3\end{bmatrix}\)= \(\begin{bmatrix} 2 & 1 & 1 \\ 5 & 4 & 4 \end{bmatrix}\)
\(\therefore (A+B)'=\) \(\begin{bmatrix} 2 & 5 \\ 1 & 4 \\ 1 &4 \end{bmatrix}\)
\(A'+B'=\) \(\begin{bmatrix} 3 & 4 \\ -1 & 2 \\ 0 &1 \end{bmatrix}\)+ \(\begin{bmatrix} -1 & 1 \\ 2 & 2 \\ 1 &3 \end{bmatrix}\)= \(\begin{bmatrix} 2 & 5 \\ 1 & 4 \\ 1 &4 \end{bmatrix}\)
Thus, we verified that:(A+B)'=A'+B'
(ii) \(A-B\)= \(\begin{bmatrix} 3 & -1 & 0 \\ 4 & 2 & 1 \end{bmatrix}\)- \(\begin{bmatrix} -1 & 2 & 1 \\ 1 &2 & 3\end{bmatrix}\) = \(\begin{bmatrix} 4 & -3 & -1 \\ 3 &0 & -2\end{bmatrix}\)
so\( (A-B)'\) = \(\begin{bmatrix} -4 & 3 \\ -3 & 0 \\ -1 &-2 \end{bmatrix}\)
A'-B'= \(\begin{bmatrix} 3 & 4 \\ -1 & 2 \\ 0 &1 \end{bmatrix}\)- \(\begin{bmatrix} -1 & 1 \\ 2 & 2 \\ 1 &3 \end{bmatrix}\)= \(\begin{bmatrix} -4 & 3 \\ -3 & 0 \\ -1 &-2 \end{bmatrix}\)
Hence we verified that: \((A-B)'=A'-B'\)
Top Questions on Matrices
Let $A = \begin{bmatrix} \cos \theta & 0 & -\sin \theta \\ 0 & 1 & 0 \\ \sin \theta & 0 & \cos \theta \end{bmatrix}$. If for some $\theta \in (0, \pi)$, $A^2 = A^T$, then the sum of the diagonal elements of the matrix $(A + I)^3 + (A - I)^3 - 6A$ is equal to
- If \(A\) is a square matrix such that \(A^2 = A\), then \((I - A)^3\) is:
Let $ A $ be a $ 3 \times 3 $ matrix such that $ | \text{adj} (\text{adj} A) | = 81.
$ If $ S = \left\{ n \in \mathbb{Z}: \left| \text{adj} (\text{adj} A) \right|^{\frac{(n - 1)^2}{2}} = |A|^{(3n^2 - 5n - 4)} \right\}, $ then the value of $ \sum_{n \in S} |A| (n^2 + n) $ is:- Let $ A $ be a matrix of order $ 3 \times 3 $ and $ |A| = 5 $. If $ |2 \, \text{adj}(3A \, \text{adj}(2A))| = 2^{\alpha} \cdot 3^{\beta} \cdot 5^{\gamma}, \quad \alpha, \beta, \gamma \in \mathbb{N} $ then $ \alpha + \beta + \gamma $ is equal to
- If \( A \) is a square matrix of order \( 3 \times 3 \), \( \det A = 3 \), then the value of \( \det(3A^{-1}) \) is:
Questions Asked in CBSE CLASS XII exam
- Using integration, find the area of the region bounded by the line \[ y = 5x + 2, \] the \( x \)-axis, and the ordinates \( x = -2 \) and \( x = 2 \).
- CBSE CLASS XII - 2025
- Evaluation of Definite Integrals by Substitution
- A 1 cm segment of a wire lying along the x-axis carries a current of 0.5 A along the \( +x \)-direction. A magnetic field \( \mathbf{B} = (0.4 \, \text{mT}) \hat{j} + (0.6 \, \text{mT}) \hat{k} \) is switched on in the region. The force acting on the segment is:
- CBSE CLASS XII - 2025
- Magnetic Effects of Current and Magnetism
The correct IUPAC name of \([ \text{Pt}(\text{NH}_3)_2\text{Cl}_2 ]^{2+} \) is:
- CBSE CLASS XII - 2025
- Coordination Compounds
- Two conductors A and B of the same material have their lengths in the ratio 1:2 and radii in the ratio 2:3. If they are connected in parallel across a battery, the ratio \( \frac{v_A}{v_B} \) of the drift velocities of electrons in them will be:
- CBSE CLASS XII - 2025
- Current electricity
- Arun, Bashir and Joseph were partners in a firm sharing profits and losses in the ratio of 5 : 3 : 2. They admitted Daksh as a new partner who acquired his share entirely from Arun. If Arun sacrificed \( \frac{1}{5} \)th from his share to Daksh, Daksh's share in the profits of the firm will be :
- CBSE CLASS XII - 2025
- Partnership Accounts
Concepts Used:
Transpose of a Matrix
The matrix acquired by interchanging the rows and columns of the parent matrix is called the Transpose matrix. The transpose matrix is also defined as - “A Matrix which is formed by transposing all the rows of a given matrix into columns and vice-versa.”
The transpose matrix of A is represented by A’. It can be better understood by the given example:
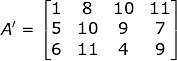
Now, in Matrix A, the number of rows was 4 and the number of columns was 3 but, on taking the transpose of A we acquired A’ having 3 rows and 4 columns. Consequently, the vertical Matrix gets converted into Horizontal Matrix.
Hence, we can say if the matrix before transposing was a vertical matrix, it will be transposed to a horizontal matrix and vice-versa.
Read More: Transpose of a Matrix