If A'=\(\begin{bmatrix}-2&3\\1&2\end{bmatrix}\)and B=\(\begin{bmatrix}-1&0\\1&2\end{bmatrix}\),then find (A+2B)'
If A'=\(\begin{bmatrix}-2&3\\1&2\end{bmatrix}\)and B=\(\begin{bmatrix}-1&0\\1&2\end{bmatrix}\),then find (A+2B)'
Solution and Explanation
We know that A=(A')'
so A=\(\begin{bmatrix}-2&1\\3&2\end{bmatrix}\)
so A+2B=\(\begin{bmatrix}-2&1\\3&2\end{bmatrix}\)+2\(\begin{bmatrix}-1&0\\1&2\end{bmatrix}\)
=\(\begin{bmatrix}-2&1\\3&2\end{bmatrix}\)+\(\begin{bmatrix}-2&0\\2&4\end{bmatrix}\)=\(\begin{bmatrix}-4&1\\5&6\end{bmatrix}\)
so (A+2B)'=\(\begin{bmatrix}-4&5\\1&6\end{bmatrix}\)
Top Questions on Matrices
- If $M$ and $N$ are square matrices of order 3 such that $\det(M) = m$ and $MN = mI$, then $\det(N)$ is equal to :
- Let \( A = \begin{bmatrix} 1 & -2 & -1 \\ 0 & 4 & -1 \\ -3 & 2 & 1 \end{bmatrix}, B = \begin{bmatrix} -5 \\ -2 \end{bmatrix}, C = [9 \ \ 7], \) which of the following is defined?
- The matrix $A = \begin{bmatrix} \sqrt{5} & 0 & 0 \\ 0 & \sqrt{2} & 0 \\ 0 & 0 & \sqrt{5} \end{bmatrix}$ is an:
- If \( A \) is a square matrix of order \( 3 \times 3 \), \( \det A = 3 \), then the value of \( \det(3A^{-1}) \) is:
- If \( A \) is a square matrix of order 2 such that \( \text{det} = 4 \), then \( \text{det}(4 \, \text{adj} \, A) \) is equal to:
Questions Asked in CBSE CLASS XII exam
Bittu and Chintu were partners in a firm sharing profit and losses in the ratio of 4 : 3. Their Balance Sheet as at 31st March, 2024 was as follows:
On 1st April, 2024, Diya was admitted in the firm for \( \frac{1}{7} \)th share in the profits on the following terms:- (i) New profit sharing ratio between Bittu, Chintu and Diya was 3 : 3 : 1 .
- (ii) Fixed Assets were found to be overvalued by ₹ 1,40,000.
- (iii) Creditors were paid ₹ 4,20,000 in full settlement.
- (iv) Diya brought proportionate capital and ₹ 5,60,000 as her share of goodwill premium by cheque.
Prepare Revaluation Account and Partners' Capital Accounts.
- CBSE CLASS XII - 2025
- Partnership Accounts
- If \( \overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} = 0 \), \( |\overrightarrow{a}| = \sqrt{37} \), \( |\overrightarrow{b}| = 3 \), and \( |\overrightarrow{c}| = 4 \), then the angle between \( \overrightarrow{b} \) and \( \overrightarrow{c} \) is:
- Two wires of the same material and the same radius have their lengths in the ratio 2:3. They are connected in parallel to a battery which supplies a current of 15 A. Find the current through the wires.
- CBSE CLASS XII - 2025
- Current electricity
- The ratio of the number of turns of the primary to the secondary coils in an ideal transformer is 20:1. If 240 V AC is applied from a source to the primary coil of the transformer and a 6.0 \( \Omega \) resistor is connected across the output terminals, then the current drawn by the transformer from the source will be:
- CBSE CLASS XII - 2025
- Electromagnetic induction
- In a Young’s double-slit experiment, two light waves, each of intensity \( I_0 \), interfere at a point, having a path difference \( \frac{\lambda}{8} \) on the screen. Find the intensity at this point.
- CBSE CLASS XII - 2025
- Interference Of Light Waves And Young’S Experiment
Concepts Used:
Transpose of a Matrix
The matrix acquired by interchanging the rows and columns of the parent matrix is called the Transpose matrix. The transpose matrix is also defined as - “A Matrix which is formed by transposing all the rows of a given matrix into columns and vice-versa.”
The transpose matrix of A is represented by A’. It can be better understood by the given example:
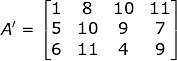
Now, in Matrix A, the number of rows was 4 and the number of columns was 3 but, on taking the transpose of A we acquired A’ having 3 rows and 4 columns. Consequently, the vertical Matrix gets converted into Horizontal Matrix.
Hence, we can say if the matrix before transposing was a vertical matrix, it will be transposed to a horizontal matrix and vice-versa.
Read More: Transpose of a Matrix