If a 10 mM solution of a biomolecule in a cuvette of path length 10 mm absorbs 90% of the incident light at 280 nm, the molar extinction coefficient of the biomolecule at this wavelength is _______ M(^{-1})cm(^{-1}). (Round off to two decimal places)
Show Hint
Solution and Explanation
Where:
- \( A \) is the absorbance.
- \( \epsilon \) is the molar extinction coefficient.
- \( c \) is the concentration in molarity.
- \( l \) is the path length in centimeters.
Given that 90% of the incident light is absorbed, the absorbance \( A \) can be calculated using:
\[ A = -\log(1 - 0.90) = -\log(0.10) = 1 \] Step 2: Given Parameters.- Concentration: \( c = 10 \) mM = \( 0.01 \) M
- Path length: \( l = 10 \) mm = \( 1 \) cm
Therefore, the molar extinction coefficient is approximately \( 100 \, \text{M}^{-1} \text{cm}^{-1} \), with reasonable estimates between 98 and 102 \( \text{M}^{-1} \text{cm}^{-1} \) based on rounding and experimental considerations.
Top Questions on Mass spectrometry
- The major product in the given reaction sequence is Q. The mass spectrum of Q shows
([M] = molecular ion peak)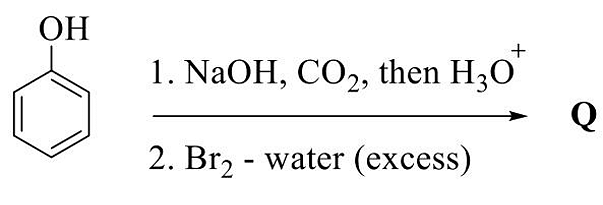
- GATE CY - 2024
- Inorganic Chemistry
- Mass spectrometry
- Which among the following characteristics of Laser light specifies the precise movement of all individual light waves together through time and space?
- AP PGECET - 2024
- Instrumentation Engineering
- Mass spectrometry
- Recombination of electron-hole produces ____ in LEDs.
- AP PGECET - 2024
- Instrumentation Engineering
- Mass spectrometry
- Magnetic sector analyzer is a part of
- AP PGECET - 2024
- Instrumentation Engineering
- Mass spectrometry
- Which ionization technique in mass spectrometry is most suitable for large biomolecules like proteins:
- GPAT - 2024
- Pharmaceutical Analysis
- Mass spectrometry
Questions Asked in GATE XL exam
- The temperature dependence of reaction rates is generally given by the Arrhenius equation. A plot of \( \ln k_r \) against \( 1/T \) is a straight line from which the pre-exponential factor ‘\( A \)’ and the activation energy ‘\( E_a \)’ can be determined.
The CORRECT option regarding this plot is:- GATE XL - 2025
- Chemical Kinetics
An electricity utility company charges ₹7 per kWh. If a 40-watt desk light is left on for 10 hours each night for 180 days, what would be the cost of energy consumption? If the desk light is on for 2 more hours each night for the 180 days, what would be the percentage-increase in the cost of energy consumption?
The \( F_{121} \) value of a known microorganism with \( Z \) value of \( 11^\circ C \) is 2.4 min for 99.9999% inactivation. For a 12D inactivation of the said microorganism at \( 143^\circ C \), the \( F \) value (in min) is .......... (rounded off to 3 decimal places)
- GATE XL - 2025
- Food Technology
- Consider a five-digit number PQRST that has distinct digits P, Q, R, S, and T, and satisfies the following conditions:
1. \( P<Q \)
2. \( S>P>T \)
3. \( R<T \)
If integers 1 through 5 are used to construct such a number, the value of P is:- GATE ST - 2025
- GATE CS - 2025
- GATE MN - 2025
- GATE XE - 2025
- GATE XL - 2025
- mathematical reasoning
Three villages P, Q, and R are located in such a way that the distance PQ = 13 km, QR = 14 km, and RP = 15 km, as shown in the figure. A straight road joins Q and R. It is proposed to connect P to this road QR by constructing another road. What is the minimum possible length (in km) of this connecting road?
Note: The figure shown is representative.