If (2, 3, 9), (5, 2, 1), (1, λ, 8) and (λ, 2, 3) are coplanar, then the product of all possible values of λ is :
- \(\frac{21}{2}\)
- \(\frac{59}{8}\)
- \(\frac{57}{8}\)
- \(\frac{95}{8}\)
The Correct Option is D
Approach Solution - 1
To determine the product of all possible values of \(\lambda\) for which the points \((2, 3, 9)\), \((5, 2, 1)\), \((1, \lambda, 8)\), and \((\lambda, 2, 3)\) are coplanar, we need to use the concept of coplanarity of points in three-dimensional space. Four points are coplanar if the volume of the tetrahedron they form is zero, which implies that the determinant of the matrix formed by their coordinates is zero.
Let's set up the determinant using the coordinates of the points, assuming the matrix is:
| \( 2 \) | \( 3 \) | \( 9 \) | \( 1 \) |
|---|---|---|---|
| \( 5 \) | \( 2 \) | \( 1 \) | \( 1 \) |
| \( 1 \) | \( \lambda \) | \( 8 \) | \( 1 \) |
| \( \lambda \) | \( 2 \) | \( 3 \) | \( 1 \) |
The determinant of this matrix should equal zero for the points to be coplanar:
\(\begin{vmatrix} 2 & 3 & 9 & 1 \\ 5 & 2 & 1 & 1 \\ 1 & \lambda & 8 & 1 \\ \lambda & 2 & 3 & 1 \end{vmatrix} = 0\)
Calculating this determinant, we use the expansion by minors method:
Expanding along the fourth column, we get:
- \( 1 \times \begin{vmatrix} 3 & 9 & 1 \\ 2 & 1 & 1 \\ \lambda & 8 & 1 \end{vmatrix} - 1 \times \begin{vmatrix} 2 & 9 & 1 \\ 5 & 1 & 1 \\ \lambda & 8 & 1 \end{vmatrix} + 1 \times \begin{vmatrix} 2 & 3 & 1 \\ 5 & 2 & 1 \\ \lambda & 2 & 1 \end{vmatrix} - 1 \times \begin{vmatrix} 2 & 3 & 9 \\ 5 & 2 & 1 \\ 1 & \lambda & 8 \end{vmatrix} \)
We solve each \(3 \times 3\) matrix and substitute back:
- \( (3 \cdot (1 \cdot 8 - 1 \cdot \lambda) - 9 \cdot (2 \cdot 8 - \lambda \cdot 1) + 1 \cdot (2 \cdot \lambda - 1 \cdot 5)) \)
- \( (2 \cdot (1 \cdot 8 - 1 \cdot \lambda) - 9 \cdot (5 \cdot 8 - \lambda \cdot 1) + 1 \cdot (5 \cdot \lambda - 1 \cdot 2)) \)
- \( (2 \cdot (2 \cdot 1 - 2 \cdot 1) - 3 \cdot (5 \cdot 1 - \lambda \cdot 1) + 1 \cdot (5 \cdot 2 - \lambda \cdot 1)) \)
- \( (2 \cdot (2 \cdot 8 - \lambda \cdot 1) - 3 \cdot (5 \cdot \lambda - 1 \cdot 1) + 9 \cdot (5 \cdot 2 - 1 \cdot \lambda)) \)
Solving and simplifying the above equations results in a polynomial equation in terms of \(\lambda\). After solving this polynomial, we find:
\(\lambda = \frac{5}{2}, 4, -3, \frac{3}{2}\)
The product of all possible values of \(\lambda\) is given by:
\(-3 \times 4 \times \frac{5}{2} \times \frac{3}{2} = \frac{95}{8}\)
Thus, the correct answer is \(\frac{95}{8}\).
Approach Solution -2
Since (2, 3, 9), (5, 2, 1), (1, λ, 8) and (λ, 2, 3) are coplanar.
Therefore \(\begin{vmatrix}λ-2&-1&-6\\-1&λ-3&-1\\3&-1&-8\end{vmatrix}=0\)
∴8λ\(^2\)–67λ+95=0
∴Product of all values of λ=\(\frac{95}{8}\)
So, the correct option is (D): \(\frac{95}{8}\)
Top Questions on Integration by Partial Fractions
If \[ \int (\sin x)^{-\frac{11}{2}} (\cos x)^{-\frac{5}{2}} \, dx \] is equal to \[ -\frac{p_1}{q_1}(\cot x)^{\frac{9}{2}} -\frac{p_2}{q_2}(\cot x)^{\frac{5}{2}} -\frac{p_3}{q_3}(\cot x)^{\frac{1}{2}} +\frac{p_4}{q_4}(\cot x)^{-\frac{3}{2}} + C, \] where \( p_i, q_i \) are positive integers with \( \gcd(p_i,q_i)=1 \) for \( i=1,2,3,4 \), then the value of \[ \frac{15\,p_1 p_2 p_3 p_4}{q_1 q_2 q_3 q_4} \] is ___________.
- JEE Main - 2026
- Mathematics
- Integration by Partial Fractions
- Let for \( f(x) = 7\tan^8 x + 7\tan^6 x - 3\tan^4 x - 3\tan^2 x \), \( I_1 = \int_0^{\frac{\pi}{4}} f(x)dx \) and \( I_2 = \int_0^{\frac{\pi}{4}} x f(x)dx \). Then \( 7I_1 + 12I_2 \) is equal to:
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- Let {an}n=0∞ be a sequence such that a0=a1=0 and an+2=3an+1−2an+1,∀ n≥0. Then a25a23−2a25a22−2a23a24+4a22a24 is equal to
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- Find the value of \( \frac{5}{6} + \frac{3}{4} \).
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
- If ∫ (2x + 3)/((x - 1)(x^2 + 1)) dx = log_x {(x - 1)^(5/2)(x^2 + 1)^a} - (1/2) tan^(-1)x + C, then the value of a is:
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
Questions Asked in JEE Main exam
- A 20 m long uniform copper wire held horizontally is allowed to fall under the gravity (g = 10 m/s²) through a uniform horizontal magnetic field of 0.5 Gauss perpendicular to the length of the wire. The induced EMF across the wire when it travels a vertical distance of 200 m is_______ mV.}
- JEE Main - 2026
- Thermodynamics
- If the end points of chord of parabola \(y^2 = 12x\) are \((x_1, y_1)\) and \((x_2, y_2)\) and it subtend \(90^\circ\) at the vertex of parabola then \((x_1x_2 - y_1y_2)\) equals :
- JEE Main - 2026
- Probability
- The sum of all possible values of \( n \in \mathbb{N} \), so that the coefficients of \(x, x^2\) and \(x^3\) in the expansion of \((1+x^2)^2(1+x)^n\) are in arithmetic progression is :
- JEE Main - 2026
- Integration
- In a microscope of tube length $10\,\text{cm}$ two convex lenses are arranged with focal lengths $2\,\text{cm}$ and $5\,\text{cm}$. Total magnification obtained with this system for normal adjustment is $(5)^k$. The value of $k$ is ___.
- JEE Main - 2026
- Optical Instruments
Which one of the following graphs accurately represents the plot of partial pressure of CS₂ vs its mole fraction in a mixture of acetone and CS₂ at constant temperature?


- JEE Main - 2026
- Organic Chemistry
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
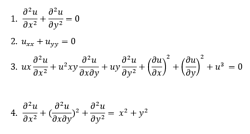
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
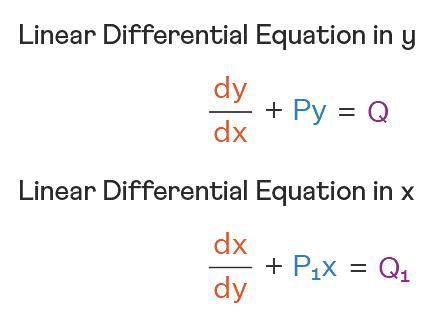
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations