For the matrices A and B, verify that (AB)′= B'A' where
(i)A=\(\begin{bmatrix}1\\-4\\3\end{bmatrix},\,B=\begin{bmatrix}-1&2&1\end{bmatrix}\)
(ii)A=\(\begin{bmatrix}0\\1\\2\end{bmatrix},\,B=\begin{bmatrix}1&5&7\end{bmatrix}\)
For the matrices A and B, verify that (AB)′= B'A' where
(i)A=\(\begin{bmatrix}1\\-4\\3\end{bmatrix},\,B=\begin{bmatrix}-1&2&1\end{bmatrix}\)
(ii)A=\(\begin{bmatrix}0\\1\\2\end{bmatrix},\,B=\begin{bmatrix}1&5&7\end{bmatrix}\)
Solution and Explanation
(i)AB=\(\begin{bmatrix}1\\-4\\3\end{bmatrix}\begin{bmatrix}-1&2&1\end{bmatrix}\)=\(\begin{bmatrix}-1&2&1\\4&-8&-4\\-3&6&3\end{bmatrix}\)
therefore (AB)'=\(\begin{bmatrix}-1&4&-3\\2&-8&6\\1&-4&3\end{bmatrix}\)
Now A'=\(\begin{bmatrix}1&-4&3\end{bmatrix}\),B'=\(\begin{bmatrix}-1\\2\\1\end{bmatrix}\)
Therefore B'A'=\(\begin{bmatrix}-1\\2\\1\end{bmatrix}=\begin{bmatrix}-1&4&-3\\2&-8&6\\1&-4&3\end{bmatrix}\)
Hence we verified that:(AB)′= B'A'
(ii)AB=\(\begin{bmatrix}0\\1\\2\end{bmatrix}\begin{bmatrix}1&5&7\end{bmatrix}\)=\(\begin{bmatrix}0&0&0\\1&5&7\\2&10&14\end{bmatrix}\)
so (AB)'=\(\begin{bmatrix}0&1&2\\0&5&10\\0&7&14\end{bmatrix}\)
Now A'=\(\begin{bmatrix}0&1&2\end{bmatrix}\),B'=\(\begin{bmatrix}1\\5\\7\end{bmatrix}\)
so B'A'=\(\begin{bmatrix}1\\5\\7\end{bmatrix}\)\(\begin{bmatrix}0&1&2\end{bmatrix}\)=\(\begin{bmatrix}0&1&2\\0&5&10\\0&7&14\end{bmatrix}\)
Hence we verified that(AB)′= B'A'
Top Questions on Matrices
- If \( A \) is a square matrix of order \( 3 \times 3 \), \( \det A = 3 \), then the value of \( \det(3A^{-1}) \) is:
- Which of the following statements is not correct?
- If A and B are two matrices such that AB is an identity matrix and the order of matrix B is \(3 \times 4\), then the order of matrix A is:
- If \(A\) is a square matrix such that \(A^2 = A\), then \((I - A)^3\) is:
- If \( B = \begin{bmatrix} 1 & 3 \\ 2 & \alpha \end{bmatrix} \) is the adjoint of a matrix \( A \) and \( |A| = 2 \), then the value of \( \alpha \) is:
Questions Asked in CBSE CLASS XII exam
The correct IUPAC name of \([ \text{Pt}(\text{NH}_3)_2\text{Cl}_2 ]^{2+} \) is:
- CBSE CLASS XII - 2025
- Coordination Compounds
- A 1 cm segment of a wire lying along the x-axis carries a current of 0.5 A along the \( +x \)-direction. A magnetic field \( \mathbf{B} = (0.4 \, \text{mT}) \hat{j + (0.6 \, \text{mT}) \hat{k} \) is switched on in the region. The force acting on the segment is:}
- CBSE CLASS XII - 2025
- Magnetic Effects of Current and Magnetism
- Using integration, find the area of the region bounded by the line \[ y = 5x + 2, \] the \( x \)-axis, and the ordinates \( x = -2 \) and \( x = 2 \).
- CBSE CLASS XII - 2025
- Evaluation of Definite Integrals by Substitution
- Two conductors A and B of the same material have their lengths in the ratio 1:2 and radii in the ratio 2:3. If they are connected in parallel across a battery, the ratio \( \frac{v_A}{v_B} \) of the drift velocities of electrons in them will be:
- CBSE CLASS XII - 2025
- Current electricity
- Arun, Bashir and Joseph were partners in a firm sharing profits and losses in the ratio of 5 : 3 : 2. They admitted Daksh as a new partner who acquired his share entirely from Arun. If Arun sacrificed \( \frac{1}{5} \)th from his share to Daksh, Daksh's share in the profits of the firm will be :
- CBSE CLASS XII - 2025
- Partnership Accounts
Concepts Used:
Transpose of a Matrix
The matrix acquired by interchanging the rows and columns of the parent matrix is called the Transpose matrix. The transpose matrix is also defined as - “A Matrix which is formed by transposing all the rows of a given matrix into columns and vice-versa.”
The transpose matrix of A is represented by A’. It can be better understood by the given example:
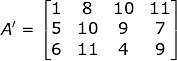
Now, in Matrix A, the number of rows was 4 and the number of columns was 3 but, on taking the transpose of A we acquired A’ having 3 rows and 4 columns. Consequently, the vertical Matrix gets converted into Horizontal Matrix.
Hence, we can say if the matrix before transposing was a vertical matrix, it will be transposed to a horizontal matrix and vice-versa.
Read More: Transpose of a Matrix