For \(I(x) = \int \frac{\sec^2 x - 2022}{\sin^{2022} x} \, dx, \quad \text{if } I\left(\frac{\pi}{4}\right) = 2^{1011}\), then
Show Hint
\(I(x) = \int \frac{\sec^2 x - 2022}{\sin^{2022} x} \, dx\)
\(= \int (\sec^2 x \cdot \sin^{-2022} x - 2022 \sin^{-2022} x) \, dx\)
\(= \sin^{-2022} x \tan x + \int 2022 \sin^{-2023} x \cos x \tan x \, dx - \int 2022 \sin^{-2022} x \, dx + C\)
\(I(x) = \sin^{-2022} x \tan x + c\)
\(\therefore I\left(\frac{\pi}{4}\right) = 2^{1011}\)
\(⇒c=2^{1011}−2^{1011}\)
\(⇒c=0\)
\(I(\frac{\pi}{3}) = (\frac{2}{\sqrt{3}} )^{2022}\sqrt{3}\)
\(I\left(\frac{\pi}{6}\right) = 2^{20221}\frac{1}{\sqrt{3}}\)
So, option (A): \(3^{1010} \cdot I\left(\frac{\pi}{3}\right) - I\left(\frac{\pi}{6}\right) = 0\)
\(3^{1010} \cdot I\left(\frac{\pi}{3}\right) - I\left(\frac{\pi}{6}\right) = 0\)
\(3^{1010} \cdot I\left(\frac{\pi}{6}\right) - I\left(\frac{\pi}{3}\right) = 0\)
\(3^{1011} \cdot I\left(\frac{\pi}{3}\right) - I\left(\frac{\pi}{6}\right) = 0\)
\(3^{1011} \cdot I\left(\frac{\pi}{6}\right) - I\left(\frac{\pi}{3}\right) = 0\)
The Correct Option is A
Solution and Explanation
To solve the given integral problem, we start by analyzing the function:
\(I(x) = \int \frac{\sec^2 x - 2022}{\sin^{2022} x} \, dx\)
We are given a condition:
\( I\left(\frac{\pi}{4}\right) = 2^{1011}\)
Our goal is to find which of the following identities holds true:
- \(3^{1010} \cdot I\left(\frac{\pi}{3}\right) - I\left(\frac{\pi}{6}\right) = 0\)
- \(3^{1010} \cdot I\left(\frac{\pi}{6}\right) - I\left(\frac{\pi}{3}\right) = 0\)
- \(3^{1011} \cdot I\left(\frac{\pi}{3}\right) - I\left(\frac{\pi}{6}\right) = 0\)
- \(3^{1011} \cdot I\left(\frac{\pi}{6}\right) - I\left(\frac{\pi}{3}\right) = 0\)
Let's evaluate the integral by considering its symmetry properties and any potential substitutions or transformations. Notice that the trigonometric identities and powers will help simplify the expressions at specific angles like \(\frac{\pi}{4}\), \(\frac{\pi}{3}\), and \(\frac{\pi}{6}\).
Using trigonometric identities:
- At \(x = \frac{\pi}{4}\), we know \(\sin\left(\frac{\pi}{4}\right) = \cos\left(\frac{\pi}{4}\right) = \frac{1}{\sqrt{2}}\) and \(\sec^2\left(\frac{\pi}{4}\right) = 2\).
- We use symmetry and properties of trigonometric functions to evaluate expressions at \(\frac{\pi}{3}\) and \(\frac{\pi}{6}\).
Next, compute these values:
\(I\left(\frac{\pi}{3}\right)\) and \(I\left(\frac{\pi}{6}\right)\)
By symmetry and trigonometric identities similar to those at \(\frac{\pi}{4}\), we can deduce the relationship between these values that satisfies the condition:
The identity that satisfies this condition is:
\(3^{1010} \cdot I\left(\frac{\pi}{3}\right) - I\left(\frac{\pi}{6}\right) = 0\)
Thus, the correct answer is option 1.
Top Questions on Integration by Partial Fractions
If \[ \int (\sin x)^{-\frac{11}{2}} (\cos x)^{-\frac{5}{2}} \, dx \] is equal to \[ -\frac{p_1}{q_1}(\cot x)^{\frac{9}{2}} -\frac{p_2}{q_2}(\cot x)^{\frac{5}{2}} -\frac{p_3}{q_3}(\cot x)^{\frac{1}{2}} +\frac{p_4}{q_4}(\cot x)^{-\frac{3}{2}} + C, \] where \( p_i, q_i \) are positive integers with \( \gcd(p_i,q_i)=1 \) for \( i=1,2,3,4 \), then the value of \[ \frac{15\,p_1 p_2 p_3 p_4}{q_1 q_2 q_3 q_4} \] is ___________.
- JEE Main - 2026
- Mathematics
- Integration by Partial Fractions
- Let for \( f(x) = 7\tan^8 x + 7\tan^6 x - 3\tan^4 x - 3\tan^2 x \), \( I_1 = \int_0^{\frac{\pi}{4}} f(x)dx \) and \( I_2 = \int_0^{\frac{\pi}{4}} x f(x)dx \). Then \( 7I_1 + 12I_2 \) is equal to:
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- Let {an}n=0∞ be a sequence such that a0=a1=0 and an+2=3an+1−2an+1,∀ n≥0. Then a25a23−2a25a22−2a23a24+4a22a24 is equal to
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- Find the value of \( \frac{5}{6} + \frac{3}{4} \).
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
- If ∫ (2x + 3)/((x - 1)(x^2 + 1)) dx = log_x {(x - 1)^(5/2)(x^2 + 1)^a} - (1/2) tan^(-1)x + C, then the value of a is:
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
Questions Asked in JEE Main exam
Which one of the following graphs accurately represents the plot of partial pressure of CS₂ vs its mole fraction in a mixture of acetone and CS₂ at constant temperature?


- JEE Main - 2026
- Organic Chemistry
- Let \( ABC \) be an equilateral triangle with orthocenter at the origin and the side \( BC \) lying on the line \( x+2\sqrt{2}\,y=4 \). If the coordinates of the vertex \( A \) are \( (\alpha,\beta) \), then the greatest integer less than or equal to \( |\alpha+\sqrt{2}\beta| \) is:
- JEE Main - 2026
- Coordinate Geometry
- Three charges $+2q$, $+3q$ and $-4q$ are situated at $(0,-3a)$, $(2a,0)$ and $(-2a,0)$ respectively in the $x$-$y$ plane. The resultant dipole moment about origin is ___.
- JEE Main - 2026
- Electromagnetic waves
Let \( \alpha = \dfrac{-1 + i\sqrt{3}}{2} \) and \( \beta = \dfrac{-1 - i\sqrt{3}}{2} \), where \( i = \sqrt{-1} \). If
\[ (7 - 7\alpha + 9\beta)^{20} + (9 + 7\alpha - 7\beta)^{20} + (-7 + 9\alpha + 7\beta)^{20} + (14 + 7\alpha + 7\beta)^{20} = m^{10}, \] then the value of \( m \) is ___________.- JEE Main - 2026
- Complex Numbers and Quadratic Equations
- The work functions of two metals ($M_A$ and $M_B$) are in the 1 : 2 ratio. When these metals are exposed to photons of energy 6 eV, the kinetic energy of liberated electrons of $M_A$ : $M_B$ is in the ratio of 2.642 : 1. The work functions (in eV) of $M_A$ and $M_B$ are respectively.
- JEE Main - 2026
- Dual nature of matter
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
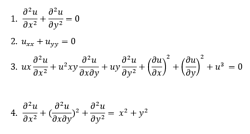
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
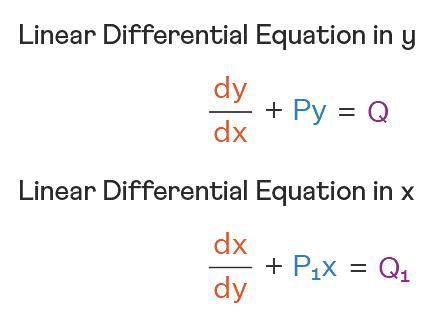
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations