Find the transpose of each of the following matrices:
I.\(\begin{bmatrix}5\\\frac{1}{2}\\-1\end {bmatrix}\)
II.\(\begin{bmatrix}1&-1\\2&3\end{bmatrix}\)
III.\(\begin{bmatrix}-1&5&6\\\sqrt3&5&6\\2&3&-1\end{bmatrix}\)
Find the transpose of each of the following matrices:
I.\(\begin{bmatrix}5\\\frac{1}{2}\\-1\end {bmatrix}\)
II.\(\begin{bmatrix}1&-1\\2&3\end{bmatrix}\)
III.\(\begin{bmatrix}-1&5&6\\\sqrt3&5&6\\2&3&-1\end{bmatrix}\)
Solution and Explanation
(i) Let A=\(\begin{bmatrix}5\\\frac{1}{2}\\-1\end {bmatrix}\)
then A-T= \(\begin{bmatrix}5&\frac{1}{2}&-1\end{bmatrix}\)
(ii)Let A= \(\begin{bmatrix}1&-1\\2&3\end{bmatrix}\)
then A-T= \(\begin{bmatrix}1&2\\-1&3\end{bmatrix}\)
(iii)Let A= \(\begin{bmatrix}-1&5&6\\\sqrt3&5&6\\2&3&-1\end{bmatrix}\)
then A-T = \(\begin{bmatrix}-1&\sqrt3&2\\5&5&3\\6&6&-1\end{bmatrix}\)
Top Questions on Matrices
- If \( A \) is a square matrix of order \( 3 \times 3 \), \( \det A = 3 \), then the value of \( \det(3A^{-1}) \) is:
- Which of the following statements is not correct?
- If A and B are two matrices such that AB is an identity matrix and the order of matrix B is \(3 \times 4\), then the order of matrix A is:
- If \(A\) is a square matrix such that \(A^2 = A\), then \((I - A)^3\) is:
- If \( B = \begin{bmatrix} 1 & 3 \\ 2 & \alpha \end{bmatrix} \) is the adjoint of a matrix \( A \) and \( |A| = 2 \), then the value of \( \alpha \) is:
Questions Asked in CBSE CLASS XII exam
The correct IUPAC name of \([ \text{Pt}(\text{NH}_3)_2\text{Cl}_2 ]^{2+} \) is:
- CBSE CLASS XII - 2025
- Coordination Compounds
- A 1 cm segment of a wire lying along the x-axis carries a current of 0.5 A along the \( +x \)-direction. A magnetic field \( \mathbf{B} = (0.4 \, \text{mT}) \hat{j + (0.6 \, \text{mT}) \hat{k} \) is switched on in the region. The force acting on the segment is:}
- CBSE CLASS XII - 2025
- Magnetic Effects of Current and Magnetism
- Using integration, find the area of the region bounded by the line \[ y = 5x + 2, \] the \( x \)-axis, and the ordinates \( x = -2 \) and \( x = 2 \).
- CBSE CLASS XII - 2025
- Evaluation of Definite Integrals by Substitution
- Two conductors A and B of the same material have their lengths in the ratio 1:2 and radii in the ratio 2:3. If they are connected in parallel across a battery, the ratio \( \frac{v_A}{v_B} \) of the drift velocities of electrons in them will be:
- CBSE CLASS XII - 2025
- Current electricity
- Arun, Bashir and Joseph were partners in a firm sharing profits and losses in the ratio of 5 : 3 : 2. They admitted Daksh as a new partner who acquired his share entirely from Arun. If Arun sacrificed \( \frac{1}{5} \)th from his share to Daksh, Daksh's share in the profits of the firm will be :
- CBSE CLASS XII - 2025
- Partnership Accounts
Concepts Used:
Transpose of a Matrix
The matrix acquired by interchanging the rows and columns of the parent matrix is called the Transpose matrix. The transpose matrix is also defined as - “A Matrix which is formed by transposing all the rows of a given matrix into columns and vice-versa.”
The transpose matrix of A is represented by A’. It can be better understood by the given example:
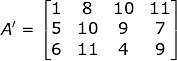
Now, in Matrix A, the number of rows was 4 and the number of columns was 3 but, on taking the transpose of A we acquired A’ having 3 rows and 4 columns. Consequently, the vertical Matrix gets converted into Horizontal Matrix.
Hence, we can say if the matrix before transposing was a vertical matrix, it will be transposed to a horizontal matrix and vice-versa.
Read More: Transpose of a Matrix