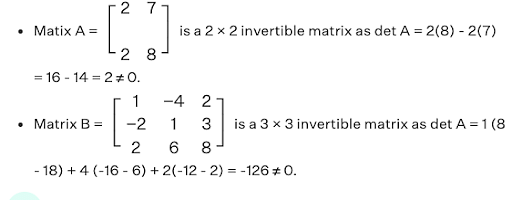Find the inverse of each of the matrices, if it exists. \(\begin{bmatrix} 1 & 3\\ 2 & 7\end{bmatrix}\)
Approach Solution - 1
Let \(A=\)\(\begin{bmatrix} 1 & 3\\ 2 & 7\end{bmatrix}\)
We know that \(A = IA\)
so\(\begin{bmatrix} 1 & 3\\ 2 & 7\end{bmatrix}\)= \(\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}A\)
⇒ \(\begin{bmatrix} 1 & 3\\ 0 & 1\end{bmatrix}\)= \(\begin{bmatrix} 1 & 0\\ -2 & 1\end{bmatrix}A\) \((R_2\rightarrow R_2-2R_1) \)
⇒ \(\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}=\begin{bmatrix} 7 & -3\\ -2 & 1 \end{bmatrix}A\) \((R_1\rightarrow R_1-3R_2) \)
\(\therefore A^{-1}\) =\(\begin{bmatrix} 7 & -3\\ -2 & 1 \end{bmatrix}\)
Approach Solution -2
\(\mathbf{A} = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\)
The inverse \(\mathbf{A}^{-1}\) is:
\(\mathbf{A}^{-1} = \frac{1}{\det(\mathbf{A})} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}\)
where \(\det(\mathbf{A})\) (the determinant of \(\mathbf{A}\)) is given by:
\(\det(\mathbf{A}) = ad - bc\)
Given the matrix:
\(\mathbf{A} = \begin{bmatrix} 1 & 3 \\ 2 & 7 \end{bmatrix}\)
First, we compute the determinant \(\det(\mathbf{A})\):
\(\det(\mathbf{A}) = (1)(7) - (3)(2) = 7 - 6 = 1\)
Since the determinant is not zero, the inverse exists. Now, we apply the formula for the inverse:
\(\mathbf{A}^{-1} = \frac{1}{\det(\mathbf{A})} \begin{bmatrix} 7 & -3 \\ -2 & 1 \end{bmatrix}\)
Substituting \(\det(\mathbf{A}) = 1\):
\(\mathbf{A}^{-1} = \frac{1}{1} \begin{bmatrix} 7 & -3 \\ -2 & 1 \end{bmatrix} = \begin{bmatrix} 7 & -3 \\ -2 & 1 \end{bmatrix}\)
So, the answer is: \(\mathbf{A}^{-1} = \begin{bmatrix} 7 & -3 \\ -2 & 1 \end{bmatrix}\)
Top Questions on Matrices
- The number of $3\times2$ matrices $A$, which can be formed using the elements of the set $\{-2,-1,0,1,2\}$ such that the sum of all the diagonal elements of $A^{T}A$ is $5$, is
- If \[ X=\begin{bmatrix}x\\y\\z\end{bmatrix} \] is a solution of the system of equations $AX=B$, where \[ \text{adj }A= \begin{bmatrix} 4 & 2 & 2\\ -5 & 0 & 5\\ 1 & -2 & 3 \end{bmatrix} \quad \text{and} \quad B=\begin{bmatrix}4\\0\\2\end{bmatrix}, \] then $|x+y+z|$ is equal to
Let \[ f(x)=\int \frac{7x^{10}+9x^8}{(1+x^2+2x^9)^2}\,dx \] and $f(1)=\frac14$. Given that

- For the matrices \( A = \begin{bmatrix} 3 & -4 \\ 1 & -1 \end{bmatrix} \) and \( B = \begin{bmatrix} -29 & 49 \\ -13 & 18 \end{bmatrix} \), if \( (A^{15} + B) \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0\\ 0 \end{bmatrix} \), then among the following which one is true?}
- Let the relation \( R \) on the set \( M = \{1, 2, 3, \ldots, 16\} \) be given by \[ R = \{(x, y) : 4y = 5x - 3,\; x, y \in M\}. \] Then the minimum number of elements required to be added in \( R \), in order to make the relation symmetric, is equal to
Questions Asked in CBSE CLASS XII exam
- Your school is organizing an Inter-House Science Model-Making Competition. As President of the Science Club, draft a notice to inform all House members from IX – XII about the competition and specify the number of registrations invited per house. Include other necessary details. You are Mitali/Mukesh. Put your notice in a box.
- CBSE CLASS XII - 2025
- Letter Writing
- The work function of a material is 2.21 eV. Which of the following cannot produce photoelectrons from it?
- CBSE CLASS XII - 2025
- Photoelectric Effect
A carpenter needs to make a wooden cuboidal box, closed from all sides, which has a square base and fixed volume. Since he is short of the paint required to paint the box on completion, he wants the surface area to be minimum.
On the basis of the above information, answer the following questions :
Find \( \frac{dS}{dx} \).- CBSE CLASS XII - 2025
- Differentiation
- A charge \( -6 \mu C \) is placed at the center B of a semicircle of radius 5 cm, as shown in the figure. An equal and opposite charge is placed at point D at a distance of 10 cm from B. A charge \( +5 \mu C \) is moved from point ‘C’ to point ‘A’ along the circumference. Calculate the work done on the charge.

- CBSE CLASS XII - 2025
- Electrostatics
- Two statements are given, one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer from the codes (A), (B), (C), and (D) as given below.
Assertion (A): In double slit experiment, if one slit is closed, diffraction pattern due to the other slit will appear on the screen.
Reason (R): For interference, at least two waves are required.
- CBSE CLASS XII - 2025
- Wave optics
Concepts Used:
Invertible matrices
A matrix for which matrix inversion operation exists, given that it satisfies the requisite conditions is known as an invertible matrix. Any given square matrix A of order n × n is called invertible if and only if there exists, another n × n square matrix B such that, AB = BA = In, where In is an identity matrix of order n × n.
For example,
It can be observed that the determinant of the following matrices is non-zero.