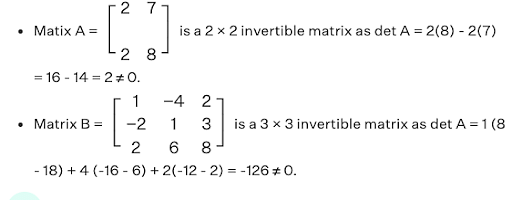Find the inverse of each of the matrices, if it exists. \(\begin{bmatrix}1&-1\\2&3\end{bmatrix}\)
Find the inverse of each of the matrices, if it exists. \(\begin{bmatrix}1&-1\\2&3\end{bmatrix}\)
Solution and Explanation
Let A= \(\begin{bmatrix}1&-1\\2&3\end{bmatrix}\) We know that A = IA
\(\therefore \begin{bmatrix}1&-1\\2&3\end{bmatrix}=\begin{bmatrix}1&0\\0&1\end{bmatrix}A\)
\(\Rightarrow\begin{bmatrix}1&-1\\0&5\end{bmatrix}=\begin{bmatrix}1&0\\-2&1\end{bmatrix}A\) (R2 \(\to\) R2-2R1)
\(\Rightarrow\begin{bmatrix}1&-1\\0&5\end{bmatrix}=\begin{bmatrix}1&0\\-\frac{2}{5}&\frac{1}{5}\end{bmatrix}A\) (R2 \(\to \frac{1}{5R_2}\))
\(\Rightarrow\begin{bmatrix}1&-1\\0&5\end{bmatrix}=\begin{bmatrix}\frac{3}{5}&\frac{1}{5}\\-\frac{2}{5}&\frac{1}{5}\end{bmatrix}A\) (R1 \(\to\) R1+R2)
so A-1= \(\begin{bmatrix}\frac{3}{5}&\frac{1}{5}\\-\frac{2}{5}&\frac{1}{5}\end{bmatrix}\)
Top Questions on Matrices
- Let \( A = \begin{bmatrix} 1 & -2 & -1 \\ 0 & 4 & -1 \\ -3 & 2 & 1 \end{bmatrix}, B = \begin{bmatrix} -5 \\ -2 \end{bmatrix}, C = [9 \ \ 7], \) which of the following is defined?
- The matrix $A = \begin{bmatrix} \sqrt{5} & 0 & 0 \\ 0 & \sqrt{2} & 0 \\ 0 & 0 & \sqrt{5} \end{bmatrix}$ is an:
- If \( A \) is a square matrix of order \( 3 \times 3 \), \( \det A = 3 \), then the value of \( \det(3A^{-1}) \) is:
- If \( A \) is a square matrix of order 2 such that \( \text{det} = 4 \), then \( \text{det}(4 \, \text{adj} \, A) \) is equal to:
- If $A$ and $B$ are two square matrices each of order 3 with $|A| = 3$ and $|B| = 5$, then $|2AB|$ is:
Questions Asked in CBSE CLASS XII exam
- If \( A = \begin{bmatrix} 1 & 0 \\ -1 & 5 \end{bmatrix} \), then find the value of \( K \) if \( A^2 = 6A + K I_2 \), where \( I_2 \) is the identity matrix.
- Account for the following: (i) Allyl chloride is hydrolyzed more readily than n-propyl chloride.
(ii) Isocyanides are formed when alkyl halides are treated with silver cyanide.
(iii) Methyl chloride reacts faster with OH$^-$ ion in $S_N2$ reaction than t-butyl chloride.- CBSE CLASS XII - 2025
- Haloalkanes And Haloarenes
- Give a chemical test to distinguish between benzaldehyde and acetophenone.
- CBSE CLASS XII - 2025
- Organic Chemistry
- Consider the arrangement shown in the figure. A black vertical arrow and a horizontal thick line with a ball are painted on a glass plate. It serves as the object. When the plate is illuminated, its real image is formed on the screen.
Which of the following correctly represents the image formed on the screen?
- CBSE CLASS XII - 2025
- Ray optics and optical instruments
- Consider two long co-axial solenoids \( S_1 \) and \( S_2 \), each of length \( l \) (\( l \gg r_2 \)) and radius \( r_1 \) and \( r_2 \) (\( r_2>r_1 \)). The number of turns per unit length are \( n_1 \) and \( n_2 \), respectively. Derive an expression for mutual inductance \( M_{12} \) of solenoid \( S_1 \) with respect to solenoid \( S_2 \). Show that \( M_{21} = M_{12} \).
- CBSE CLASS XII - 2025
- Electromagnetic induction
Concepts Used:
Invertible matrices
A matrix for which matrix inversion operation exists, given that it satisfies the requisite conditions is known as an invertible matrix. Any given square matrix A of order n × n is called invertible if and only if there exists, another n × n square matrix B such that, AB = BA = In, where In is an identity matrix of order n × n.
For example,
It can be observed that the determinant of the following matrices is non-zero.