Distance between twice-magnified virtual image of an object placed in front of mirror is 15 cm. Find focal length of spherical mirror in cm.
Correct Answer: 10
Solution and Explanation
Top Questions on Spherical Mirrors
- A concave mirror produces an image of an object such that the distance between the object and image is 20 cm. If the magnification of the image is \( -3 \), then the magnitude of the radius of curvature of the mirror is:
- JEE Main - 2025
- Physics
- Spherical Mirrors
- (ii) An object at a distance of 16 cm from a spherical mirror forms a virtual image at a distance of 12 cm behind the mirror. Determine the magnification of the image and type of the mirror.
- UP Board X - 2025
- Science
- Spherical Mirrors
- Image of an object formed by a concave mirror is real and of the size of the object. The object is placed -
- UP Board X - 2025
- Science
- Spherical Mirrors
- With the help of a suitable ray diagram, derive the formula \( \frac{1}{v} + \frac{1}{u} = \frac{1}{f} \) for a concave mirror.
- UP Board XII - 2025
- Physics
- Spherical Mirrors
- The length of the image formed by a concave mirror:
- UP Board XII - 2025
- Physics
- Spherical Mirrors
Questions Asked in JEE Main exam
- Let \( f: \mathbb{R} \to \mathbb{R} \) be a function defined by \( f(x) = \left( 2 + 3a \right)x^2 + \left( \frac{a+2}{a-1} \right)x + b, a \neq 1 \). If \[ f(x + y) = f(x) + f(y) + 1 - \frac{2}{7}xy, \] then the value of \( 28 \sum_{i=1}^5 f(i) \) is:
- JEE Main - 2025
- Functions
Let $ f: \mathbb{R} \to \mathbb{R} $ be a twice differentiable function such that $$ f''(x)\sin\left(\frac{x}{2}\right) + f'(2x - 2y) = (\cos x)\sin(y + 2x) + f(2x - 2y) $$ for all $ x, y \in \mathbb{R} $. If $ f(0) = 1 $, then the value of $ 24f^{(4)}\left(\frac{5\pi}{3}\right) $ is:
- JEE Main - 2025
- Differential Calculus
- A 400 g solid cube having an edge of length \(10\) cm floats in water. How much volume of the cube is outside the water? (Given: density of water = \(1000 { kg/m}^3\))
- An infinite wire has a circular bend of radius \( a \), and carrying a current \( I \) as shown in the figure. The magnitude of the magnetic field at the origin \( O \) of the arc is given by:

- JEE Main - 2025
- Magnetic Field
- Let \( A = [a_{ij}] \) be a matrix of order 3 \(\times\) 3, with \(a_{ij} = (\sqrt{2})^{i+j}\). If the sum of all the elements in the third row of \( A^2 \) is \( \alpha + \beta\sqrt{2} \), where \(\alpha, \beta \in \mathbb{Z}\), then \(\alpha + \beta\) is equal to:
- JEE Main - 2025
- Matrices and Determinants
Concepts Used:
Spherical Mirrors
A spherical mirror is a mirror which has been cut out of a spherical surface.
There are two kinds of spherical mirrors:
- Convex Mirror
- Concave Mirror
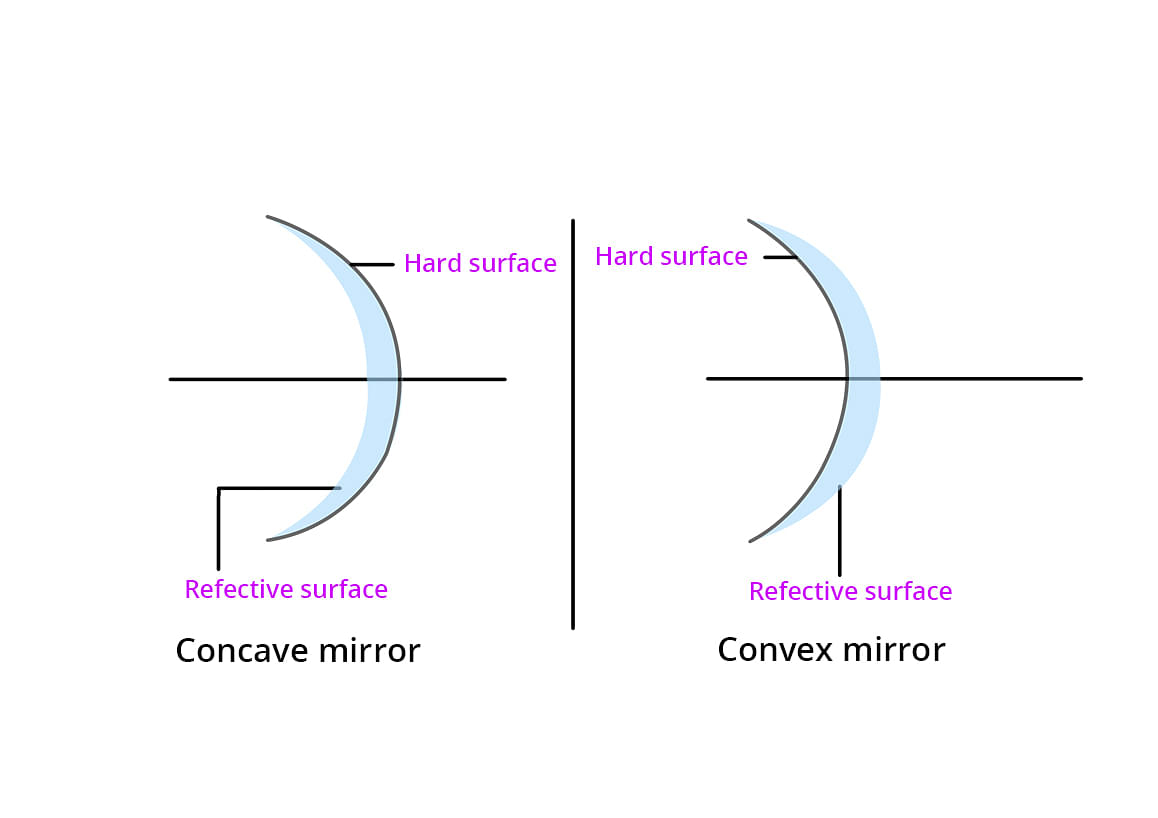
Concave Mirror
Concave mirrors are also called converging mirrors, because in these types of mirrors, light rays converge at a point after impact and reflect back from the reflective surface of the mirror.
Convex Mirror
The convex mirror has a reflective surface that is curved outward. Regardless of the distance between the subject and the mirrors, these mirrors are "always" virtual, upright and reduced.