Consider two radionuclides P and Q. Suppose the half-life of P (\( t_{1/2}^P \)) is four times that of Q (\( t_{1/2}^Q \)). At time \( t = 0 \), there are \( N_0 \) atoms of both radionuclides. When will the radioactivity of the two radionuclides be equal?
Show Hint
- \( t = t_{1/2}^P \)
- \( t = 0.66\, t_{1/2}^P \)
- \( t = 0.75\, t_{1/2}^P \)
- \( t = 1.5\, t_{1/2}^P \)
The Correct Option is B
Solution and Explanation
Decay constant is related to half-life as:
\[ \lambda = \frac{\ln 2}{t_{1/2}} \]
Given \( t_{1/2}^P = 4 t_{1/2}^Q \), we get:
\[ \lambda_P = \frac{\ln 2}{4 t_{1/2}^Q}, \quad \lambda_Q = \frac{\ln 2}{t_{1/2}^Q} \]
Thus,
\[ \lambda_Q = 4\lambda_P \]
Step 2: Write radioactivity expressions.
Radioactivity:
\[ A(t) = \lambda N(t) \]
\[ N(t) = N_0 e^{-\lambda t} \]
So radioactivities are:
\[ A_P(t) = \lambda_P N_0 e^{-\lambda_P t} \]
\[ A_Q(t) = \lambda_Q N_0 e^{-\lambda_Q t} \]
Step 3: Set the activities equal.
\[ \lambda_P e^{-\lambda_P t} = \lambda_Q e^{-\lambda_Q t} \]
\[ e^{-(\lambda_Q - \lambda_P)t} = \frac{\lambda_P}{\lambda_Q} \]
\[ e^{-3\lambda_P t} = \frac{1}{4} \]
Step 4: Take natural logarithm.
\[ -3\lambda_P t = -\ln 4 \]
\[ t = \frac{\ln 4}{3\lambda_P} \]
Step 5: Substitute \( \lambda_P = \frac{\ln 2}{t_{1/2}^P} \).
\[ t = \frac{\ln 4}{3} \cdot \frac{t_{1/2}^P}{\ln 2} \]
Since \( \ln 4 = 2\ln 2 \):
\[ t = \frac{2\ln 2}{3\ln 2} \, t_{1/2}^P \]
\[ t = \frac{2}{3} t_{1/2}^P \]
\[ t \approx 0.66\, t_{1/2}^P \]
Step 6: Conclusion.
Thus, the radioactivity of P and Q becomes equal at
\[ t = 0.66\, t_{1/2}^P \]
Hence, the correct answer is (B).
Top Questions on X Rays and the Ordering of the Elements
- The shortest wavelength, present in X-rays produced by an accelerating potential of 50kV, is:
- CUET (PG) - 2025
- Material Science and Technology
- X Rays and the Ordering of the Elements
- In Laue's technique of X-ray diffraction, a single crystal is held stationary and the beam of white radiation of wavelength \(\lambda\) is inclined at which condition with glancing angle (\(\theta\)):
- CUET (PG) - 2025
- Material Science and Technology
- X Rays and the Ordering of the Elements
- The minimum wavelength of X-rays produced by 20 keV electrons is nearly
- AP EAPCET - 2025
- Physics
- X Rays and the Ordering of the Elements
- An X-ray beam of initial intensity I0 of 70 keV imaging the chest is assumed to undergo attenuation through the muscle tissue for a thickness of 16 cm and further through the bone tissue for a thickness of 4 cm. The half value layer (HVL) thicknesses for the muscle and bone are 3.5 cm and 1.8 cm, respectively. The percentage of X-ray intensity transmitted through the body is ________.
Give your answer rounded off to 2 decimal places.- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
- The X-ray attenuation coefficients as a function of photon energy for three materials are shown in the figure below. A tissue phantom containing these three materials is imaged at two different X-ray photon energies of 50 keV and 150 keV. When the developed X-ray film is viewed, which of the following statements is/are TRUE ?
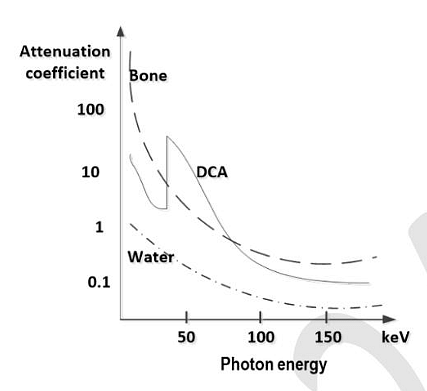
- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
Questions Asked in GATE BM exam
A Wheatstone bridge is used to measure strain as shown in the figure below.
Initially, the bridge was balanced. When a strain is applied to the resistor \( R_{{strain}} \), along its length, the output voltage \( V_{{out}} \) is 10 mV. If \( R_{{strain}} \) is a cylindrical resistor of length \( l \) and cross-sectional area \( A \), the magnitude of the applied strain is _______.
(rounded off to two decimal places)
- GATE BM - 2025
- Decay processes
An ideal, massless spring with spring constant 1 N/m (upper panel of the given figure) is cut into 5 equal parts. If two of these parts are connected in parallel (lower panel of the given figure), what is the resultant spring constant in N/m? (rounded off to the nearest integer)

- GATE BM - 2025
- Phase Shift Keying (PSK)
The plot of \( \log_{10} ({BMR}) \) as a function of \( \log_{10} (M) \) is a straight line with slope 0.75, where \( M \) is the mass of the person and BMR is the Basal Metabolic Rate. If a child with \( M = 10 \, {kg} \) has a BMR = 600 kcal/day, the BMR for an adult with \( M = 100 \, {kg} \) is _______ kcal/day. (rounded off to the nearest integer)

- GATE BM - 2025
- Positron Emission Tomography
For the RLC circuit shown below, the root mean square current \( I_{{rms}} \) at the resonance frequency is _______amperes. (rounded off to the nearest integer)

\[ V_{{rms}} = 240 \, {V}, \quad R = 60 \, \Omega, \quad L = 10 \, {mH}, \quad C = 8 \, \mu {F} \]- GATE BM - 2025
- Electrical Circuits
The frequency of the oscillator circuit shown in the figure below is _______(in kHz, rounded off to two decimal places).

Given: \( R = 1 \, k\Omega; R_1 = 2 \, k\Omega; R_2 = 6 \, k\Omega; C = 0.1 \, \mu F \)- GATE BM - 2025
- Phase Shift Keying (PSK)