Consider a series of steps as shown. A ball is thrown from 0. Find the minimum speed to directly jump to 5th step
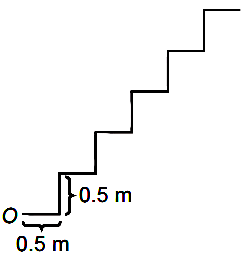
Consider a series of steps as shown. A ball is thrown from 0. Find the minimum speed to directly jump to 5th step
- \(5(\sqrt2+1) m/s\)
- \(5(\sqrt2) m/s\)
- \(5(\sqrt{(\sqrt2+1))} m/s\)
- \(6(\sqrt3+1) m/s\)
The Correct Option is C
Solution and Explanation
The Correct option is (C): \(5(\sqrt{(\sqrt2+1))} m/s\)
\(y=x\tan\theta-\frac{gx^2}{2v^2\cos^2\theta}\)
(2.5,2.5) must lie on this
\(⇒1=\tan\theta-\frac{g\times2.5}{2v^2\cos^2\theta}\)
\(⇒ \frac{25}{2v^2\cos^2\theta}=\tan\theta-1\)
\(⇒ v^2=\frac{25}{2}\left\{\frac{1+\tan^2\theta}{\tan\theta-1}\right\}\)
\(⇒ v_{min}=5\sqrt{\sqrt2+1}\)
[ Happens when \(\tan\theta=\sqrt2+1\) ]
Top Questions on Speed and velocity
- Earth has mass 8 times and radius 2 times that of a planet. If the escape velocity from the earth is 11.2 km/s, the escape velocity in km/s from the planet will be:
- JEE Main - 2025
- Physics
- Speed and velocity
- A fluid flows through a pipe with varying cross-section. If the velocity at the narrow section is 3 m/s and the cross-sectional area is half of the wider section, what is the velocity in the wider section?
- BITSAT - 2025
- Physics
- Speed and velocity
- A ball of mass \(120\) \(g\) moving with initial velocity \(25 \;m/s\) is stopped by an external force \(F\) in \(0.15\) \(sec\). Find value of \(F\) in newton :
- JEE Main - 2024
- Physics
- Speed and velocity
- Two trains run on North-South parallel tracks. Train A moves with velocity 20 m/s towards North and train B moves with velocity 30 m/s towards South. Then find the velocity of train B with respect to train A
- JEE Main - 2024
- Physics
- Speed and velocity
- A uniform disk of mass \(50\) \(kg\) is rolling without slipping with a speed of \(0.4 \;m/s\). Find minimum energy required to bring the disk to rest (in \(J\)).
- JEE Main - 2024
- Physics
- Speed and velocity
Questions Asked in JEE Main exam
Which one of the following graphs accurately represents the plot of partial pressure of CS₂ vs its mole fraction in a mixture of acetone and CS₂ at constant temperature?


- JEE Main - 2026
- Organic Chemistry
- Let \( ABC \) be an equilateral triangle with orthocenter at the origin and the side \( BC \) lying on the line \( x+2\sqrt{2}\,y=4 \). If the coordinates of the vertex \( A \) are \( (\alpha,\beta) \), then the greatest integer less than or equal to \( |\alpha+\sqrt{2}\beta| \) is:
- JEE Main - 2026
- Coordinate Geometry
- Three charges $+2q$, $+3q$ and $-4q$ are situated at $(0,-3a)$, $(2a,0)$ and $(-2a,0)$ respectively in the $x$-$y$ plane. The resultant dipole moment about origin is ___.
- JEE Main - 2026
- Electromagnetic waves
Let \( \alpha = \dfrac{-1 + i\sqrt{3}}{2} \) and \( \beta = \dfrac{-1 - i\sqrt{3}}{2} \), where \( i = \sqrt{-1} \). If
\[ (7 - 7\alpha + 9\beta)^{20} + (9 + 7\alpha - 7\beta)^{20} + (-7 + 9\alpha + 7\beta)^{20} + (14 + 7\alpha + 7\beta)^{20} = m^{10}, \] then the value of \( m \) is ___________.- JEE Main - 2026
- Complex Numbers and Quadratic Equations
- The work functions of two metals ($M_A$ and $M_B$) are in the 1 : 2 ratio. When these metals are exposed to photons of energy 6 eV, the kinetic energy of liberated electrons of $M_A$ : $M_B$ is in the ratio of 2.642 : 1. The work functions (in eV) of $M_A$ and $M_B$ are respectively.
- JEE Main - 2026
- Dual nature of matter
Concepts Used:
Speed and Velocity
The rate at which an object covers a certain distance is commonly known as speed.
The rate at which an object changes position in a certain direction is called velocity.
Difference Between Speed and Velocity:

Read More: Difference Between Speed and Velocity