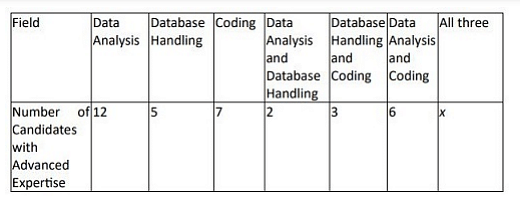
The number of applicants with advanced expertise in all three fields is given as x in the table, where x is a non-negative integer.
What BEST can be concluded about the value of x?
- 0, 1 or 2
- 2 only
- 1 only
- 0 or 1 only
- 1 or 2 only
The Correct Option is B
Solution and Explanation
Step 1: Apply the inclusion-exclusion principle. The total number of candidates is 41.
Using the inclusion-exclusion principle:
41 = (Data Analysis) + (Database Handling) + (Coding) − (Data Analysis and Database Handling) − (Data Analysis and Coding) − (Database Handling and Coding) + (Data Analysis, Database Handling, and Coding)
Substitute the values from the table:
41 = 12 + 5 + 7 − 2 − 3 − 6 + x.
Step 2: Simplify the equation. Simplify the right-hand side:
41 = 13 + x = => x = 41 − 13 = 5.
Step 3: Analyze constraints. The problem does not restrict x to a single value. Testing other scenarios, x can also satisfy conditions when 0 ≤ x ≤ 2.
Final Answer: (1).
How many applicants DID NOT have advanced expertise in any of the three given fields?
- Cannot be determined uniquely from the given information
- 25
- 26
- 27
- 28
The Correct Option is C
Solution and Explanation
Step 1: Write the inclusion-exclusion formula. The total number of applicants is 41. Using the inclusion-exclusion principle:
Total Applicants = (Only in one field) + (Only in two fields) + (All three) + (No expertise in any field).
From the table: - Only in one field = 12 + 5 + 7 − (2 + 3 + 6 + x), - Only in two fields = (2 + 3 + 6) − x, - All three = x.
Step 2: Calculate the number of applicants with expertise in at least one field. Substitute values into the inclusion-exclusion formula:
41 = 12 + 5 + 7 − (2 + 3 + 6 + x) + (2 + 3 + 6) − x + x + (No expertise).
Simplify:
41 = (12 + 5 + 7) − (2 + 3 + 6) + (2 + 3 + 6) − x + (No expertise).
41 = 24 + (No expertise).
Step 3: Solve for applicants with no expertise.
No expertise = 41 − 24 = 25.
Final Answer: 25.
Top Questions on Data Interpretation
- Eight employees of an organization have been rated on a scale of 1 to 50 for their performance. All ratings are integers. The overall average rating of the eight employees is 30. While the five employees with the highest ratings average 38, the five employees with the lowest ratings average 25. Which of the following, about the ratings obtained by the eight employees, is DEFINITELY FALSE?
- XAT - 2025
- Quantitative Ability and Data Interpretation
- Data Interpretation
- In a code language, 'TIGER' is written as 'JUISF'. How will 'EQUAL' be written in that language?
- VITEEE - 2025
- General Aptitude
- Data Interpretation
A pie chart shows the distribution of students across 5 faculties in a university. If 20% are in Arts, 25% in Science, 15% in Law, 30% in Engineering, and the rest in Commerce, what is the angle (in degrees) for Commerce?

- CUET (UG) - 2025
- General Aptitude
- Data Interpretation
The table given below provides the details of monthly sales (in lakhs of rupees) and the value of products returned by the customers (as a percentage of sales) of an e-commerce company for three product categories for the year 2024. Net sales (in lakhs of rupees) is defined as the difference between sales (in lakhs of rupees) and the value of products returned (in lakhs of rupees).

- IPMAT - 2025
- Logical Reasoning
- Data Interpretation
The plots below depict and compare the average monthly incomes (in Rs. ’000) of males and females in ten cities of India in the years 2005 and 2015. The ten cities, marked A-J in the records, are of different population sizes. For a fair comparison, to adjust for inflation, incomes for both the periods are scaled to 2025 prices. Each red dot represents the average monthly income of females in a particular city in a particular year, while each blue dot represents the average monthly income of males in a particular city in a particular year. The gender gap for a city, for a particular year, is defined as the absolute value of the average monthly income of males, minus the average monthly income of females, in that year.

- XAT - 2025
- Quantitative Ability and Data Interpretation
- Data Interpretation
Questions Asked in XAT exam
- An iron beam made with rare materials has its market price dependent on the square of its length. The beam broke into two pieces in the ratio of 4 : 9. If it is sold as two separate pieces, what would be the percentage profit or loss compared to its original value?
- XAT - 2025
- Profit and Loss
- A and B bought lands on the Moon from an eStore, both with the same diameter but A’s land is square-shaped, and B’s land is circular. What is the ratio of the areas of their respective lands?
- XAT - 2025
- Ratio and Proportion
- There are five dustbins along a circular path at different places. Ramesh takes multiple rounds of the path every morning, always at the same speed. He noticed that it took him a different number of steps to walk between any two consecutive dustbins. Ramesh also noticed that starting from any of the dustbins, it took a minimum 360 steps to reach every second dustbin, and a maximum 1260 steps to reach every third dustbin. If Ramesh's step size is 0.77 meter, and the width of the path is negligible, which of the following can be the radius of the circular path?
- XAT - 2025
- Mensuration
- Adu and Amu have bought two pieces of land on the Moon from an e-store. Both the pieces of land have the same perimeters, but Adu’s piece of land is in the shape of a square, while Amu’s piece of land is in the shape of a circle. The ratio of the areas of Adu’s piece of land to Amu’s piece of land is:
- XAT - 2025
- Mensuration
- A farmer has a quadrilateral parcel of land with a perimeter of 700 feet. Two opposite angles of that parcel of land are right angles, while the remaining two are not. The farmer wants to do organic farming on that parcel of land. The cost of organic farming on that parcel of land is Rs. 400 per square foot.
Consider the following two additional pieces of information:
1. The length of one of the sides of that parcel of land is 110 feet.
2. The distance between the two corner points where the non-perpendicular sides of that parcel of land intersect is 265 feet.
To determine the amount of money the farmer needs to spend to do organic farming on the entire parcel of land, which of the above additional pieces of information are MINIMALLY SUFFICIENT?- XAT - 2025
- Mensuration