An α particle and a proton are accelerated from rest through the same potential difference. The ratio of linear momenta acquired by above two particles will be:
- √2:1
- 2√2:1
- 4√2:1
- 8:1
The Correct Option is B
Solution and Explanation
The ratio of linear momenta acquired by above two particles,
\(\frac{pα}{pp}=\frac{\sqrt{2(4m)(2eV)}}{{\sqrt{2(m)(eV)}}}\)
\(=\frac{\sqrt{16}}{√2}\)
=\(\frac{4}{√2}\)
\(=\frac{2√2}{1}\)
So, the correct option is (B): \(\frac{2√2}{1}\)
Top Questions on centripetal acceleration
- A particle is moving with a constant velocity of 5 m/s in a circular path of radius 2 m. What is the centripetal acceleration of the particle?
- MHT CET - 2025
- Physics
- centripetal acceleration
- A body of mass 0.2 kg is attached to a light string of length 1 m and revolved in a vertical circle. What is the minimum speed at the lowest point so that the body can complete the circular motion? (Take \( g = 10 \, \text{m/s}^2 \))
- MHT CET - 2025
- Physics
- centripetal acceleration
- A body moves in a circle of radius \( r = 5 \, \text{m} \) with a constant speed of \( v = 10 \, \text{m/s} \). What is the centripetal acceleration of the body?
- MHT CET - 2025
- Physics
- centripetal acceleration
- A particle is moving in a circle of radius 2 m with a constant speed of 4 m/s. What is the centripetal acceleration?
- MHT CET - 2025
- Physics
- centripetal acceleration
A parallel plate capacitor with air between the plates has a capacitance of 4 pF. If the distance between the plates is reduced by half and the space between them is filled with a substance of dielectric constant 6, then the value of capacitance will be ……..
- GUJCET - 2024
- Physics
- centripetal acceleration
Questions Asked in JEE Main exam
- Let \( y = f(x) \) be the solution of the differential equation\[\frac{dy}{dx} + \frac{xy}{x^2 - 1} = \frac{x^6 + 4x}{\sqrt{1 - x^2}}, \quad -1 < x < 1\] such that \( f(0) = 0 \). If \[6 \int_{-1/2}^{1/2} f(x)dx = 2\pi - \alpha\] then \( \alpha^2 \) is equal to __________.
- JEE Main - 2025
- Differential equations
- Marks obtained by all the students of class 12 are presented in a frequency distribution with classes of equal width. Let the median of this grouped data be 14 with median class interval 12-18 and median class frequency 12. If the number of students whose marks are less than 12 is 18, then the total number of students is:
- JEE Main - 2025
- Statistics
- Let the system of equations $ x + 5y - z = 1 $ $ 4x + 3y - 3z = 7 $ $ 24x + y + \lambda z = \mu $ where $ \lambda, \mu \in \mathbb{R} $, have infinitely many solutions. Then the number of the solutions of this system, if $x, y, z$ are integers and satisfy $7 \leq x + y + z \leq 77$, is:
- JEE Main - 2025
- Linear Systems and Determinants
- A force of 49 N acts tangentially at the highest point of a sphere (solid of mass 20 kg) kept on a rough horizontal plane. If the sphere rolls without slipping, then the acceleration of the center of the sphere is:
- JEE Main - 2025
- Quantum Mechanics
Match List-I with List-II: List-I
- JEE Main - 2025
- Classification Of Organic Compounds
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
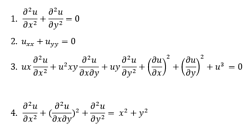
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
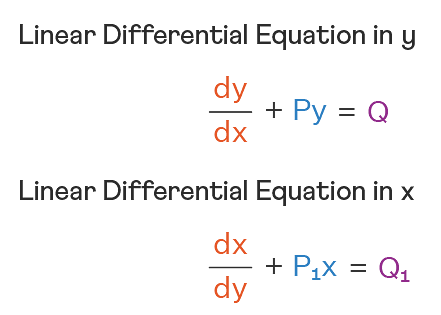
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations