A wide slab consisting of two media of refractive indices $n_{1}$ and $n_{2}$ is placed in air as shown in the figure A ray of light is incident from medium $n _{1}$ to $n _{2}$ at an angle $\theta$, where $\sin \theta$ is slightly larger than $\frac1 { n _{1}}$ Take refractive index of air as $1$ Which of the following statement(s) is(are) correct?
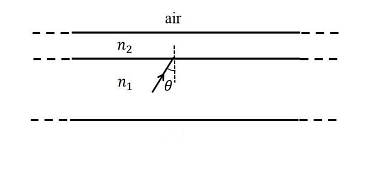
- The light ray enters air if $n_{2}=n_{1}$
- The light ray is finally reflected back into the medium of refractive index $n _{1}$ if $n _{2}< n _{1}$
- The light ray is finally reflected back into the medium of refractive index $n_{1}$ if $n_{2}>n_{1}$
- The light ray is reflected back into the medium of refractive index $n_{1}$ if $n_{2}=1$
The Correct Option is D
Solution and Explanation
The correct answer is option (D): The light ray is reflected back into the medium of refractive index $n_{1}$ if $n_{2}=1$
Top Questions on Ray optics and optical instruments
- A thin prism \( P_1 \) with angle \( 4^\circ \) made of glass having refractive index 1.54 is combined with another thin prism \( P_2 \) made of glass having refractive index 1.72 to get dispersion without deviation. The angle of the prism \( P_2 \) in degrees is:
- JEE Main - 2025
- Physics
- Ray optics and optical instruments
- A hemispherical vessel is completely filled with a liquid of refractive index \( \mu \). A small coin is kept at the lowest point \( O \) of the vessel as shown in the figure. The minimum value of the refractive index of the liquid so that a person can see the coin from point \( E \) (at the level of the vessel) is:
- JEE Main - 2025
- Physics
- Ray optics and optical instruments
Given below are two statements. One is labelled as Assertion (A) and the other is labelled as Reason (R):
Assertion (A): An electron in a certain region of uniform magnetic field is moving with constant velocity in a straight line path.
Reason (R): The magnetic field in that region is along the direction of velocity of the electron.In the light of the above statements, choose the correct answer from the options given below:
- JEE Main - 2025
- Physics
- Ray optics and optical instruments
- A long straight wire of a circular cross-section with radius \( a \) carries a steady current \( I \). The current is uniformly distributed across this cross-section. The plot of magnitude of magnetic field \( B \) with distance \( r \) from the centre of the wire is given by:
- JEE Main - 2025
- Physics
- Ray optics and optical instruments
- The focal length of a concave mirror in air is \( f \). When the mirror is immersed in a liquid of refractive index \( \frac{3}{5} \), its focal length will become:
- CBSE CLASS XII - 2025
- Physics
- Ray optics and optical instruments
Questions Asked in JEE Advanced exam
- Let \(S=\left\{\begin{pmatrix} 0 & 1 & c \\ 1 & a & d\\ 1 & b & e \end{pmatrix}:a,b,c,d,e\in\left\{0,1\right\}\ \text{and} |A|\in \left\{-1,1\right\}\right\}\), where |A| denotes the determinant of A. Then the number of elements in S is _______.
- JEE Advanced - 2024
- Matrices
- A positive, singly ionized atom of mass number \( A_M \) is accelerated from rest by the voltage \( 192 \, \text{V} \). Thereafter, it enters a rectangular region of width \( w \) with magnetic field \( \vec{B}_0 = 0.1\hat{k} \, \text{T} \). The ion finally hits a detector at the distance \( x \) below its starting trajectory. Which of the following option(s) is(are) correct? \[ \text{(Given: Mass of neutron/proton = } \frac{5}{3} \times 10^{-27} \, \text{kg, charge of the electron = } 1.6 \times 10^{-19} \, \text{C).} \]
- JEE Advanced - 2024
- Electromagnetic Field (EMF)
- A thin stiff insulated metal wire is bent into a circular loop with its two ends extending tangentially from the same point of the loop. The wire loop has mass \( m \) and radius \( r \) and is in a uniform vertical magnetic field \( B_0 \). When a current \( I \) is passed through the loop, the loop turns about the line PQ by an angle \( \theta \). The angle \( \theta \) is given by:
- JEE Advanced - 2024
- Electromagnetic Field (EMF)
- A region in the form of an equilateral triangle (in x-y plane) of height \( L \) has a uniform magnetic field \( \mathbf{B} \) pointing in the \( +z \)-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height \( L \), is placed in the x-y plane with its vertex \( P \) at \( x = 0 \) in the orientation shown in the figure. At \( t = 0 \), the loop starts entering the region of the magnetic field with a uniform velocity \( \mathbf{v} \) along the \( +x \)-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
Which of the following graphs best depicts the variation of the induced emf (\( \mathcal{E} \)) in the loop as a function of the distance (\( x \)) starting from \( x = 0 \)?- JEE Advanced - 2024
- Radioactivity
- A table tennis ball has radius \( \frac{3}{2} \times 10^{-2} \, \text{m} \) and mass \( \frac{22}{7} \times 10^{-3} \, \text{kg} \). It is slowly pushed down into a swimming pool to a depth \( d = 0.7 \, \text{m} \) below the water surface and then released from rest. It emerges from the water surface at speed \( v \), without getting wet, and rises to a height \( H \). Which of the following option(s) is(are) correct?\(\text{(Given: } \pi = \frac{22}{7}, g = 10 \, \text{m/s}^2, \text{density of water} = 1 \times 10^3 \, \text{kg/m}^3, \text{viscosity of water} = 1 \times 10^{-3} \, \text{Pa.s).}\)
- JEE Advanced - 2024
- Radioactivity
Concepts Used:
Ray Optics and Optical Instruments
Optics, deals with the determination of behaviour and the properties of light, along with its interactions with the matter and also with the instruments that are used to detect it.
Ray optics is also known as the geometrical optics and it is a branch of science which describes light propagation.
Reflection is the change in direction of light at an interface in-between two different media so that the wave-front returns into a medium from which it was originated.
Speed of light is the rate at which the light travels in free space.
A phenomenal change in image formed when the light is passed from one medium to another which is called Refraction.
Total Internal Reflection is the reflection of light when the light ray enters into a rarer medium from a denser medium and the angle of incidence is higher than the critical angle of incidence then that light ray will be reflected back to the denser medium.
Read More: Ray Optics and Optical Instruments