Question

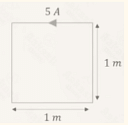
The current of 5 A flows in a square loop of sides 1 m placed in air. The magnetic field at the center of the loop is \(X\sqrt{2} \times 10^{-7} \, T\). The value of X = _________.

Answer 1

Correct Answer: 40

This problem requires us to calculate the magnetic field at the center of a square current-carrying loop and then determine the value of a constant \( X \) from the given expression for the magnetic field.

Concept Used:

The magnetic field \( B \) at a point P, due to a straight wire of finite length carrying a current \( I \), at a perpendicular distance \( d \) from the wire is given by the Biot-Savart law application:

\[ B = \frac{\mu_0 I}{4\pi d} (\sin\theta_1 + \sin\theta_2) \]

where \( \theta_1 \) and \( \theta_2 \) are the angles subtended by the ends of the wire at point P. For a square loop, the total magnetic field at the center is the sum of the magnetic fields due to its four sides. By symmetry, the field from each side is identical in magnitude and direction.

\[ B_{\text{center}} = 4 \times B_{\text{one side}} \]

Step-by-Step Solution:

Step 1: Identify the given parameters.

Current in the loop, \( I = 5 \, \text{A} \).

Side length of the square loop, \( L = 1 \, \text{m} \).

The loop is in air, so we use the permeability of free space, \( \mu_0 = 4\pi \times 10^{-7} \, \text{T}\cdot\text{m/A} \).

Step 2: Determine the geometry for calculating the field from one side.

The perpendicular distance \( d \) from the center of the square to the midpoint of any side is half the side length.

\[ d = \frac{L}{2} = \frac{1}{2} = 0.5 \, \text{m} \]

The angles \( \theta_1 \) and \( \theta_2 \) subtended by the ends of a side at the center are equal. The diagonals of a square bisect at \( 90^\circ \), so the lines from the center to the vertices of a side make angles of \( 45^\circ \) with the perpendicular from the center to that side.

\[ \theta_1 = \theta_2 = 45^\circ \]

Step 3: Calculate the magnetic field due to one side of the square loop.

Using the formula for a finite wire:

\[ B_{\text{one side}} = \frac{\mu_0 I}{4\pi d} (\sin 45^\circ + \sin 45^\circ) \]

Substitute the values:

\[ B_{\text{one side}} = \frac{(4\pi \times 10^{-7}) \times 5}{4\pi \times 0.5} \left(\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}\right) \] \[ B_{\text{one side}} = \frac{5 \times 10^{-7}}{0.5} \left(\frac{2}{\sqrt{2}}\right) \] \[ B_{\text{one side}} = 10 \times 10^{-7} \times \sqrt{2} = \sqrt{2} \times 10^{-6} \, \text{T} \]

Step 4: Calculate the total magnetic field at the center of the loop.

The total magnetic field is four times the field from a single side.

\[ B_{\text{center}} = 4 \times B_{\text{one side}} \] \[ B_{\text{center}} = 4 \times (\sqrt{2} \times 10^{-6}) = 4\sqrt{2} \times 10^{-6} \, \text{T} \]

To match the given format, we can write this as:

\[ B_{\text{center}} = 40\sqrt{2} \times 10^{-7} \, \text{T} \]

Step 5: Compare the calculated magnetic field with the given expression to find X.

The problem states that the magnetic field at the center is \( X\sqrt{2} \times 10^{-7} \, \text{T} \).

\[ X\sqrt{2} \times 10^{-7} = 40\sqrt{2} \times 10^{-7} \]

By comparing both sides of the equation, we find:

\[ X = 40 \]

The value of X is 40.