Question:
A source of sound emits sound waves at frequency \( f_0 \). It is moving towards an observer with fixed speed \( v_s \) (\( v_s < v \), where \( v \) is the speed of sound in air). If the observers were to move towards the source with speed \( v_0 \), one of the following two graphs (A and B) will give the correct variation of the frequency \( f \) heard by the observer as \( v_0 \) changes.

A source of sound emits sound waves at frequency \( f_0 \). It is moving towards an observer with fixed speed \( v_s \) (\( v_s < v \), where \( v \) is the speed of sound in air). If the observers were to move towards the source with speed \( v_0 \), one of the following two graphs (A and B) will give the correct variation of the frequency \( f \) heard by the observer as \( v_0 \) changes.
Show Hint
For moving sources and observers, the Doppler effect formula is critical for understanding frequency shifts. Pay attention to the relative speeds involved.
Updated On: Apr 18, 2025
- Graph A with slope \( \frac{f_0}{v + v_s} \)
- Graph B with slope \( \frac{f_0}{v - v_s} \)
- Graph A with slope \( \frac{f_0}{v - v_s} \)
- Graph B with slope \( \frac{f_0}{v + v_s} \)
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The Doppler effect equation for frequency heard by an observer moving towards a source is given by: \[ f = f_0 \frac{v + v_0}{v - v_s} \] This formula indicates that the frequency \( f \) increases as the observer approaches the source. The slope of the graph \( f \) with respect to \( v_0 \) (observer’s speed) is: \[ \text{slope} = \frac{f_0}{v - v_s} \] Thus, graph A is the correct choice.
Was this answer helpful?
0
0
Top Questions on doppler effect
- When both the source of sound and observer approach each other with a speed equal to 10% of the speed of sound, then the percentage change in frequency heard by the observer is nearly
- AP EAPCET - 2025
- Physics
- doppler effect
- A passenger is sitting in a fast moving train. The engine of the train blows a whistle of frequency N. If the apparent frequency of sound heard by the passengers is \( N' \), then:
- MHT CET - 2025
- Physics
- doppler effect
- A source (S) of sound has frequency\( 240 Hz\). When the observer (O) and the source move towards each other at a speed \(v\) with respect to the ground (as shown in Case 1 in the figure), the observer measures the frequency of the sound to be \(288 Hz\). However, when the observer and the source move away from each other at the same speed v with respect to the ground (as shown in Case 2 in the figure), the observer measures the frequency of sound to be \(n\) Hz. The value of \(n\) is _____.
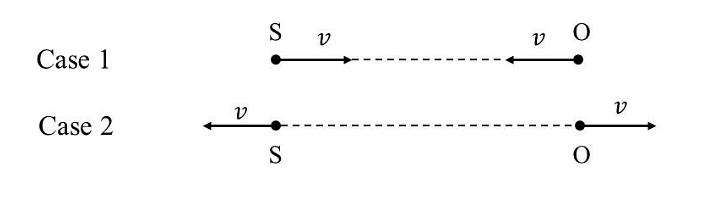
- JEE Advanced - 2024
- Physics
- doppler effect
- A galaxy is moving away from the Earth so that a spectral line at 6000 Å is observed at 6300 Å. Then the speed of the galaxy with respect to the Earth is
- KCET - 2024
- Physics
- doppler effect
- A train is moving with a speed of \(10 m/s\) towards a platform and blows a horn with frequency \(400 Hz\). Find the frequency heard by a passenger standing on the platform. Take speed of sound = \(310 m/s\).
- JEE Main - 2023
- Physics
- doppler effect
View More Questions
Questions Asked in COMEDK UGET exam
- The magnetic flux linked with a coil is given by the equation: $ \phi = 8t^2 + t + 10 $ The e.m.f. induced in the coil in the 3rd second will be
- COMEDK UGET - 2024
- Electromagnetic induction
- A satellite is revolving around the earth in a circular orbit with kinetic energy of $1.69 \times 10^{10}$ J. The additional kinetic energy required for just escaping into the outer space is
- COMEDK UGET - 2024
- Escape Speed
A solid cylinder of mass 2 kg and radius 0.2 m is rotating about its own axis without friction with angular velocity 5 rad/s. A particle of mass 1 kg moving with a velocity of 5 m/s strikes the cylinder and sticks to it as shown in figure.

The angular velocity of the system after the particle sticks to it will be:- COMEDK UGET - 2024
- The Angular Momentum
- In a given semiconductor, the ratio of the number density of electron to number density of hole is 2 : 1. If $ \frac{1}{7} $th of the total current is due to the hole and the remaining is due to the electrons, the ratio of the drift velocity of holes to the drift velocity of electrons is :
- COMEDK UGET - 2024
- Semiconductors
- A transformer which steps down 330 V to 33 V is to operate a device having impedance 110 $\Omega$. The current drawn by the primary coil of the transformer is:
- COMEDK UGET - 2024
- Transformers
View More Questions