Question:
A source and a detector move away from each other in absence of wind with a speed of 20 m/s with respect to the ground. If the detector detects a frequency of 1800 Hz of the sound coming from the source, then the original frequency of source considering speed of sound in air 340 m/s will be _________ Hz.
A source and a detector move away from each other in absence of wind with a speed of 20 m/s with respect to the ground. If the detector detects a frequency of 1800 Hz of the sound coming from the source, then the original frequency of source considering speed of sound in air 340 m/s will be _________ Hz.
Show Hint
Mnemonic: For frequency, "Observer on Top, Source at Bottom". If distance increases, frequency decreases; so subtract from the top and add to the bottom.
Updated On: Dec 31, 2025
Hide Solution
Verified By Collegedunia
Correct Answer: 2025
Solution and Explanation
Step 1: Understanding the Concept:
The Doppler Effect explains the change in observed frequency due to the relative motion between the source and the observer. When they move away from each other, the observed frequency is lower than the actual frequency.
Step 2: Key Formula or Approach:
General Doppler formula: \(f' = f \left( \frac{v \pm v_d}{v \mp v_s} \right)\).
When both move away: \(f' = f \left( \frac{v - v_d}{v + v_s} \right)\).
Step 3: Detailed Explanation:
Given:
Apparent frequency \(f' = 1800 \text{ Hz}\).
Speed of sound \(v = 340 \text{ m/s}\).
Speed of source \(v_s = 20 \text{ m/s}\).
Speed of detector \(v_d = 20 \text{ m/s}\).
Using the formula for moving away:
\[ 1800 = f \left( \frac{340 - 20}{340 + 20} \right) \]
\[ 1800 = f \left( \frac{320}{360} \right) \]
\[ 1800 = f \left( \frac{8}{9} \right) \]
\[ f = 1800 \times \frac{9}{8} \]
\[ f = 225 \times 9 = 2025 \text{ Hz} \]
Step 4: Final Answer:
The original frequency of the source is 2025 Hz.
The Doppler Effect explains the change in observed frequency due to the relative motion between the source and the observer. When they move away from each other, the observed frequency is lower than the actual frequency.
Step 2: Key Formula or Approach:
General Doppler formula: \(f' = f \left( \frac{v \pm v_d}{v \mp v_s} \right)\).
When both move away: \(f' = f \left( \frac{v - v_d}{v + v_s} \right)\).
Step 3: Detailed Explanation:
Given:
Apparent frequency \(f' = 1800 \text{ Hz}\).
Speed of sound \(v = 340 \text{ m/s}\).
Speed of source \(v_s = 20 \text{ m/s}\).
Speed of detector \(v_d = 20 \text{ m/s}\).
Using the formula for moving away:
\[ 1800 = f \left( \frac{340 - 20}{340 + 20} \right) \]
\[ 1800 = f \left( \frac{320}{360} \right) \]
\[ 1800 = f \left( \frac{8}{9} \right) \]
\[ f = 1800 \times \frac{9}{8} \]
\[ f = 225 \times 9 = 2025 \text{ Hz} \]
Step 4: Final Answer:
The original frequency of the source is 2025 Hz.
Was this answer helpful?
0
0
Top Questions on doppler effect
- A passenger is sitting in a fast moving train. The engine of the train blows a whistle of frequency N. If the apparent frequency of sound heard by the passengers is \( N' \), then:
- MHT CET - 2025
- Physics
- doppler effect
- When both the source of sound and observer approach each other with a speed equal to 10% of the speed of sound, then the percentage change in frequency heard by the observer is nearly
- AP EAPCET - 2025
- Physics
- doppler effect
- A source (S) of sound has frequency\( 240 Hz\). When the observer (O) and the source move towards each other at a speed \(v\) with respect to the ground (as shown in Case 1 in the figure), the observer measures the frequency of the sound to be \(288 Hz\). However, when the observer and the source move away from each other at the same speed v with respect to the ground (as shown in Case 2 in the figure), the observer measures the frequency of sound to be \(n\) Hz. The value of \(n\) is _____.
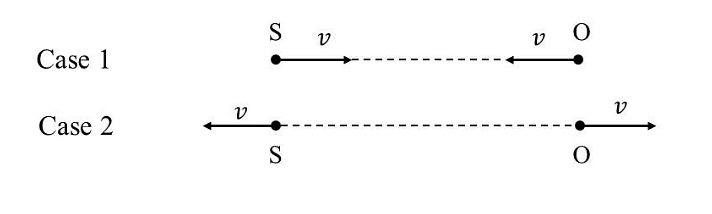
- JEE Advanced - 2024
- Physics
- doppler effect
- A galaxy is moving away from the Earth so that a spectral line at 6000 Å is observed at 6300 Å. Then the speed of the galaxy with respect to the Earth is
- KCET - 2024
- Physics
- doppler effect
- A train is moving with a speed of \(10 m/s\) towards a platform and blows a horn with frequency \(400 Hz\). Find the frequency heard by a passenger standing on the platform. Take speed of sound = \(310 m/s\).
- JEE Main - 2023
- Physics
- doppler effect
View More Questions
Questions Asked in JEE Main exam
- The system of linear equations
$x + y + z = 6$
$2x + 5y + az = 36$
$x + 2y + 3z = b$
has- JEE Main - 2026
- Matrices and Determinants
- The displacement of a particle executing simple harmonic motion with time period \(T\) is expressed as \[ x(t)=A\sin\omega t, \] where \(A\) is the amplitude of oscillation. If the maximum value of the potential energy of the oscillator is found at \[ t=\frac{T}{2\beta}, \] then the value of \(\beta\) is ________.
- JEE Main - 2026
- Waves and Oscillations
- A complex number 'z' satisfy both \(|z-6|=5\) & \(|z+2-6i|=5\) simultaneously. Find the value of \(z^3 + 3z^2 - 15z + 141\).
- JEE Main - 2026
- Algebra
In the given figure, the blocks $A$, $B$ and $C$ weigh $4\,\text{kg}$, $6\,\text{kg}$ and $8\,\text{kg}$ respectively. The coefficient of sliding friction between any two surfaces is $0.5$. The force $\vec{F}$ required to slide the block $C$ with constant speed is ___ N.
(Given: $g = 10\,\text{m s}^{-2}$)
- JEE Main - 2026
- Rotational Mechanics
Two circular discs of radius \(10\) cm each are joined at their centres by a rod, as shown in the figure. The length of the rod is \(30\) cm and its mass is \(600\) g. The mass of each disc is also \(600\) g. If the applied torque between the two discs is \(43\times10^{-7}\) dyne·cm, then the angular acceleration of the system about the given axis \(AB\) is ________ rad s\(^{-2}\).

- JEE Main - 2026
- Rotational motion
View More Questions