A small square loop of wire of side l is placed inside a large square loop of wire L(L>>l). As shown in figure, both loops are coplanar and their centers coincide at point O. The mutual inductance of the system is:
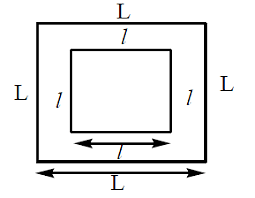

\(\frac{2\sqrt2 \mu_0L^2}{\pi l}\)
\(\frac{\mu_0L^2}{2\sqrt2 \pi L}\)
\(\frac{2\sqrt 2 \mu_0 l^2}{\pi L}\)
\(\frac{\mu_0L^2}{2\sqrt2\pi l}\)
The Correct Option is C
Solution and Explanation
B1=4B=\(\frac{4μ_0i}{4π(\frac{L}{2})(2sin45°)}\)
B1=\(\frac{2\sqrt 2 \mu_0 l^2}{\pi L}\)
M=\(\frac{Flux inner loop}{i}\)=\(\frac{2\sqrt 2 \mu_0 il^2}{i\pi ^2}\)
=\(\frac{2\sqrt2 \mu_0l^2}{\pi L}\)
Top Questions on Inductance
- If an inductor coil of self-inductance 2H stores 25J of magnetic energy, then the current passing through it is:
- KEAM - 2025
- Physics
- Inductance
- The dimensions of the coefficient of self-inductance are:
- BITSAT - 2024
- Physics
- Inductance
- If \( L \) is the inductance and \( R \) is the resistance, then the unit of \( \frac{L}{R} \) is:
- MHT CET - 2024
- Physics
- Inductance
- A coil of inductance \( L \) is divided into 6 equal parts. All these parts are connected in parallel. The resultant inductance of this combination is:
- AP EAMCET - 2024
- Physics
- Inductance
- The current passing through a coil of 120 turns and inductance \( 40 \) mH is \( 30 \) mA. The magnetic flux linked with the coil is:
- AP EAMCET - 2024
- Physics
- Inductance
Questions Asked in JEE Main exam
- 500 J of energy is transferred as heat to 0.5 mol of Argon gas at 298 K and 1.00 atm. The final temperature and the change in internal energy respectively are: Given \( R = 8.3 \, \text{J K}^{-1} \text{mol}^{-1} \).
- JEE Main - 2025
- Thermodynamics
- The value of \( (\sin 70^\circ)(\cot 10^\circ \cot 70^\circ - 1) \) is:
- JEE Main - 2025
- Trigonometric Identities
- A conducting bar moves on two conducting rails as shown in the figure. A constant magnetic field \( B \) exists into the page. The bar starts to move from the vertex at time \( t = 0 \) with a constant velocity. If the induced EMF is \( E \propto t^n \), then the value of \( n \) is ________________________.

- JEE Main - 2025
- Electromagnetic induction
- A radioactive nucleus \( n_2 \) has 3 times the decay constant as compared to the decay constant of another radioactive nucleus \( n_1 \). If the initial number of both nuclei are the same, what is the ratio of the number of nuclei of \( n_2 \) to the number of nuclei of \( n_1 \), after one half-life of \( n_1 \)?
- JEE Main - 2025
- Radioactive Decay
- Assume a living cell with 0.9%(\(w/w\)) of glucose solution (aqueous). This cell is immersed in another solution having equal mole fraction of glucose and water. (Consider the data up to first decimal place only) The cell will:
- JEE Main - 2025
- osmosis
Concepts Used:
Inductance
Inductance is a key parameter in electrical and electronic circuit designs. Like resistance and capacitance, it is a basic electrical measurement that affects all circuits to some degree.
Inductance is used in many areas of electrical and electronic systems and circuits. The electronic components can be in a variety of forms and may be called by a variety of names: coils, inductors, chokes, transformers, . . . Each of these may also have a variety of different variants: with and without cores and the core materials may be of different types.
There are two ways in which inductance is used:
- Self-inductance: Self-inductance is the property of a circuit, often a coil, whereby a change in current causes a change in voltage in that circuit due to the magnetic effect of caused by the current flow. It can be seen that self-inductance applies to a single circuit - in other words it is an inductance, typically within a single coil. This effect is used in single coils or chokes.
- Mutual-inductance: Mutual inductance is an inductive effect where a change in current in one circuit causes a change in voltage across a second circuit as a result of a magnetic field that links both circuits. This effect is used in transformers.