Question:
A particle moving along the x-axis approaches π₯=0 from π₯ =ββ with a total energy E. It is subjected to a potential π(π₯). For time π‘ββ, the probability density P(x) of the particle is schematically shown in the figure.
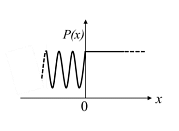
The correct option for the potential π(π₯) is:
A particle moving along the x-axis approaches π₯=0 from π₯ =ββ with a total energy E. It is subjected to a potential π(π₯). For time π‘ββ, the probability density P(x) of the particle is schematically shown in the figure.
The correct option for the potential π(π₯) is:
The correct option for the potential π(π₯) is:
Updated On: Jan 12, 2025
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
For a particle moving through a potential with a given energy, the probability density \( P(x) \) represents the likelihood of finding the particle at a given position. The potential that produces the required probability distribution in the figure should have the corresponding characteristics based on the energy \( E \) and the nature of the particleβs behavior.
Option (C) matches the required potential shape.
Was this answer helpful?
0
0
Top Questions on Waves and Oscillations
- The displacement of a particle executing simple harmonic motion with time period \(T\) is expressed as \[ x(t)=A\sin\omega t, \] where \(A\) is the amplitude of oscillation. If the maximum value of the potential energy of the oscillator is found at \[ t=\frac{T}{2\beta}, \] then the value of \(\beta\) is ________.
- JEE Main - 2026
- Physics
- Waves and Oscillations
Using a variable frequency ac voltage source the maximum current measured in the given LCR circuit is 50 mA for V = 5 sin (100t) The values of L and R are shown in the figure. The capacitance of the capacitor (C) used is_______ Β΅F.
- JEE Main - 2026
- Physics
- Waves and Oscillations
- A cylindrical block of mass $M$ and area of cross section $A$ is floating in a liquid of density $\rho$ with its axis vertical. When depressed a little and released the block starts oscillating. The period of oscillation is ___.
- JEE Main - 2026
- Physics
- Waves and Oscillations
- Using a simple pendulum experiment $g$ is determined by measuring its time period $T$. Which of the following plots represent the correct relation between the pendulum length $L$ and time period $T$?
- JEE Main - 2026
- Physics
- Waves and Oscillations
- A body of mass 2 kg is moving along x-direction such that its displacement as function of time is given by $x(t) = \alpha t^2 + \beta t + \gamma$ m, where $\alpha = 1$ m/s$^2$, $\beta = 1$ m/s and $\gamma = 1$ m. The work done on the body during the time interval $t = 2$ s to $t = 3$ s, is _________ J.
- JEE Main - 2026
- Physics
- Waves and Oscillations
View More Questions
Questions Asked in IIT JAM exam
- Consider a volume V enclosed by a closed surface S having unit surface normal \(\hat{n}\). For \(\mathbf{r} = x\hat{i} + y\hat{j} + z\hat{k}\), the value of the surface integral \(\frac{1}{9} \oint_{S} \mathbf{r} \cdot \hat{n} \,dS\) is
- IIT JAM PH - 2025
- Vector Calculus
- For a Zener diode as shown in the circuit diagram below, the Zener voltage \(V_Z\) is 3.7 V. For a load resistance (\(R_L\)) of 1 k\(\Omega\), a current \(I_1\) flows through the load. If \(R_L\) is decreased to 500 \(\Omega\), the current changes to \(I_2\). The ratio \(\frac{I_2}{I_1}\) is \rule{1cm{0.15mm}. (up to two decimal places)}
- IIT JAM PH - 2025
- Analog Electronics
- The shortest distance between an object and its real image formed by a thin convex lens of focal length 20 cm is _____ cm. (in integer)
- If \(\left(\frac{1-i}{1+i}\right)^{n/2} = -1\), where \(i = \sqrt{-1}\), one possible value of n is
- IIT JAM PH - 2025
- Complex numbers
- In a two-level atomic system, the excited state is 0.2 eV above the ground state. Considering the Maxwell-Boltzmann distribution, the temperature at which 2% of the atoms will be in the excited state is _____ K. (up to two decimal places)
(Boltzmann constant \(k_B = 8.62 \times 10^{-5}\) eV/K)
- IIT JAM PH - 2025
- Mechanics
View More Questions