Question

Consider a thick biconvex lens (thickness t=4cm and refractive index n=1.5) whose magnitudes of the radii of curvature R1 and R2, of the first and second surfaces are 30cm and 20cm, respectively. Surface 2 is silvered to act as a mirror. A point object is placed at point A on the axis (OA= 60cm) as shown in the figure. If its image is formed at point Q, the distance d between O and Q is_____ cm. (Rounded off to two decimal places)

Answer 1

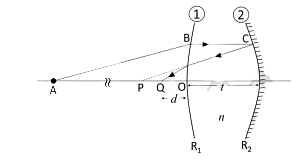
Correct Answer: 3.55

Calculation of the Focal Length of a Thick Lens

The focal length \( f_L \) of the thick lens can be calculated using the lensmaker’s formula for a thick lens:

\[ \frac{1}{f_L} = (n-1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right) + \frac{(n-1) t}{n R_1 R_2} \]

where:

• \( n = 1.5 \) (refractive index)
• \( t = 4 \) cm (thickness of the lens)
• \( R_1 = 30 \) cm (radius of curvature of the first surface)
• \( R_2 = -20 \) cm (radius of curvature of the second surface)

Step 1: Substituting the Given Values

\[ \frac{1}{f_L} = (1.5 - 1) \left( \frac{1}{30} - \frac{1}{-20} \right) + \frac{(1.5 - 1) \cdot 4}{1.5 \cdot 30 \cdot (-20)} \]

Step 2: Simplifying the Terms

\[ \frac{1}{f_L} = 0.5 \left( \frac{1}{30} + \frac{1}{20} \right) + \frac{0.5 \times 4}{1.5 \times 30 \times (-20)} \]

Calculating the individual terms:

• \( \frac{1}{30} = 0.0333 \)
• \( \frac{1}{20} = 0.05 \)
• \( \frac{0.5 \times 4}{1.5 \times 30 \times (-20)} = \frac{2}{-900} = -0.0022 \)

Step 3: Summing the Terms

\[ \frac{1}{f_L} = 0.5 (0.0333 + 0.05 - 0.0022) = 0.5 \times 0.0811 = 0.04055 \]

Thus, the focal length of the lens is:

\[ f_L = \frac{1}{0.04055} \approx 24.67 \text{ cm} \]

Calculation of the Equivalent Focal Length of the Lens-Mirror System

The equivalent focal length \( F \) of the lens-mirror system is given by:

\[ \frac{1}{F} = \frac{1}{f_L} + \frac{2}{f_m} \]

where the focal length of the mirror is:

\[ f_m = \frac{R_2}{2} = \frac{-20}{2} = -10 \text{ cm} \]

Step 4: Substituting the Values

\[ \frac{1}{F} = \frac{1}{24.67} + \frac{2}{-10} \]

\[ \frac{1}{F} = 0.04055 - 0.2 = -0.15945 \]

Thus, the equivalent focal length is:

\[ F = \frac{1}{-0.15945} \approx -6.27 \text{ cm} \]

Calculation of Image Distance

The object distance from the lens-mirror system is:

\[ u = -60 \text{ cm} \]

Using the lens formula for the system:

\[ \frac{1}{F} = \frac{1}{v} - \frac{1}{u} \]

Step 5: Substituting the Values

\[ \frac{1}{-6.27} = \frac{1}{v} - \frac{1}{-60} \]

Step 6: Solving for \( v \)

Rearranging the equation:

\[ -0.15945 = \frac{1}{v} + 0.01667 \]

\[ \frac{1}{v} = -0.15945 - 0.01667 = -0.17612 \]

Thus, the image distance is:

\[ v = \frac{1}{-0.17612} \approx -5.68 \text{ cm} \]

Calculation of Distance \( d \) Between O and Q

The distance \( d \) between \( O \) and \( Q \) is given by:

\[ d = |v| - t \]

Substituting the values:

\[ d = 5.68 - 4.00 = 3.50 \text{ cm} \]

Final Answer

The distance \( d \) between \( O \) and \( Q \) is 3.50 cm.