Prove: \(∫_1^3\frac {dx}{x^2(x+1)}=\frac 23+log\frac 23\)
Solution and Explanation
Let \(I=\)\(∫_1^3\frac {dx}{x^2(x+1)}=\frac 23+log\frac 23\)
Also, let \(\frac {1}{x^2(x+1)}\) = \(\frac Ax+\frac {B}{x^2}+\frac {C}{x+1}\)
\(⇒I=Ax(x+1)+B(x+1)+C(x^2)\)
\(⇒I=Ax^2+Ax+Bx+Cx^2\)
Equating the coefficients of \( x^2,x,\) and constant term, we obtain
\(A+C=0\)
\(A+B=0\)
\(B=1\)
On solving these equations, we obtain
\(A=-1,C=1,\ and \ B=1\)
∴\(\frac {1}{x^2(x+1)}\) = \(-\frac 1x+\frac {1}{x^2}+\frac {1}{x+1}\)
\(⇒I\) = \(∫_1^3\)\([-\frac 1x+\frac {1}{x^2}+\frac {1}{x+1}]dx\)
\(I\)= \([-logx-\frac 1x+log(x+1)]_1^3\)
\(I\)= \([log(\frac {x+1}{x})-\frac 1x]_1^3\)
\(I\)= \(log(\frac 43)-\frac 13-log(\frac 21)+1\)
\(I\)= \( log\ 4-log\ 3-log\ 2+\frac 23\)
\(I\)= \(log\ 2-log\ 3+\frac 23\)
\(I\)= \(log(\frac 23)+\frac 23\)
Hence, the given result is proved.
Top Questions on integral
- Let \( y = f(x) \) be a thrice differentiable function in \( (-5, 5) \). Let the tangents to the curve \( y = f(x) \) at \( (1, f(1)) \) and \( (3, f(3)) \) make angles \( \frac{\pi}{6} \) and \( \frac{\pi}{4} \), respectively, with the positive x-axis. If \(2 \int_{\frac{1}{\sqrt{3}}}^{1} \left( \left( f'(t) \right)^2 + 1 \right) f''(t) \, dt = \alpha + \beta \sqrt{3}\) where \( \alpha \), \( \beta \) are integers, then the value of \( \alpha + \beta \) equals
- Let $f : (0, \infty) \to \mathbb{R}$ and $F(x) = \int_{0}^{x} tf(t) \, dt$. If $F(x^2) = x^4 + x^5$, then \[\sum_{r=1}^{12} f(r^2)\]is equal to:
- If \[\int_{0}^{\frac{\pi}{3}} \cos^4 x \, dx = a\pi + b\sqrt{3},\]where $a$ and $b$ are rational numbers, then $9a + 8b$ is equal to:
- The value of \[\int_{0}^{1} \left(2x^3 - 3x^2 - x + 1\right)^{\frac{1}{3}} \, dx\]is equal to:
- Let \( r_k = \frac{\int_{0}^{1} (1 - x^7)^k \, dx}{\int_{0}^{1} (1 - x^7)^{k+1} \, dx}, \, k \in \mathbb{N} \). Then the value of \[ \sum_{k=1}^{10} \frac{1}{7(r_k - 1)}\]is equal to ______.
Questions Asked in CBSE CLASS XII exam
- Find the inverse of each of the matrices, if it exists. \(\begin{bmatrix} 1 & 3\\ 2 & 7\end{bmatrix}\)
- For what values of x,\(\begin{bmatrix} 1 & 2 & 1 \end{bmatrix}\)\(\begin{bmatrix} 1 & 2 & 0\\ 2 & 0 & 1 \\1&0&2 \end{bmatrix}\)\(\begin{bmatrix} 0 \\2\\x\end{bmatrix}\)=O?
- Find the inverse of each of the matrices,if it exists \(\begin{bmatrix} 2 & 1 \\ 7 & 4 \end{bmatrix}\)
What is the Planning Process?
- CBSE CLASS XII - 2023
- Planning process steps
- Find the inverse of each of the matrices,if it exists. \(\begin{bmatrix} 2 & 3\\ 5 & 7 \end{bmatrix}\)
Concepts Used:
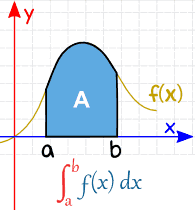
Definite Integral
Definite integral is an operation on functions which approximates the sum of the values (of the function) weighted by the length (or measure) of the intervals for which the function takes that value.
Definite integrals - Important Formulae Handbook
A real valued function being evaluated (integrated) over the closed interval [a, b] is written as :
\(\int_{a}^{b}f(x)dx\)
Definite integrals have a lot of applications. Its main application is that it is used to find out the area under the curve of a function, as shown below:
