Integrate the function: \(\frac{1}{x^{\frac{1}{2}}+x^{\frac{1}{3}}}\) [Hint:\(\frac{1}{x^{\frac{1}{2}}+x^{\frac{1}{3}}}\)=\(\frac{1}{x^{\frac{1}{3}(1+x^{\frac{1}{6}})}}\)Put x=t6]
Solution and Explanation
\(\frac{1}{x^{\frac{1}{2}}+x^{\frac{1}{3}}}\)=\(\frac{1}{x^{\frac{1}{3}(1+x^{\frac{1}{6}})}}\)
Let x=t6⇒dx=6t5dt
∴\(\int \frac{1}{x^{\frac{1}{2}}+x^{\frac{1}{3}}}dx=\frac{1}{x^{\frac{1}{3}(1+x^{\frac{1}{6}})}}dx\)
=∫6t5/t2(1+t)dt
=6∫\(\frac{t^3}{1+t}dt\)
Top Questions on integral
- Evaluate the integral: $$ \int_0^{\pi/4} \frac{\ln(1 + \tan x)}{\cos x \sin x} \, dx $$
- Find the value of the integral: \[ \int_0^\pi \sin^2(x) \, dx. \]
- Evaluate the integral \( \int_0^1 \frac{\ln(1 + x)}{1 + x^2} \, dx \)
- Evaluate the integral: $$ \int_0^1 \frac{\ln (1+x)}{1+x^2} \, dx $$
- Evaluate $ \int_{0}^{1} (3x^2 + 2x) \, dx $.
Questions Asked in CBSE CLASS XII exam
Both the poems, ‘My Mother at Sixty-six’ and ‘Aunt Jennifer’s Tigers,’ delve into experiences of life. How do these poems bring out the internal conflict in each of the women?
- CBSE CLASS XII - 2025
- Aunt Jennifer's Tigers
How do the stories ‘The Last Lesson’ by Alphonse Daudet and ‘Lost Spring’ by Anees Jung illustrate the impact of socio-political factors on education?
- CBSE CLASS XII - 2025
- Lost Spring
The author vividly describes the trauma of Zitkala-Sa and Bama in 'Memories of Childhood’. Support with examples from the texts, to illustrate the prejudices that were present in society.
- CBSE CLASS XII - 2025
- memories of childhood
How did Dr. Sadao plan the American prisoner’s escape? (The Enemy)
- CBSE CLASS XII - 2025
- The enemy pearl
- What could be the reason for the disintegration of Gondwana? \hfill \textit{(Journey to the End of the Earth)
- CBSE CLASS XII - 2025
- Journey to the end of the earth
Concepts Used:
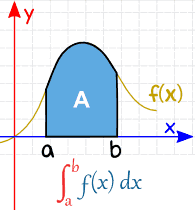
Definite Integral
Definite integral is an operation on functions which approximates the sum of the values (of the function) weighted by the length (or measure) of the intervals for which the function takes that value.
Definite integrals - Important Formulae Handbook
A real valued function being evaluated (integrated) over the closed interval [a, b] is written as :
\(\int_{a}^{b}f(x)dx\)
Definite integrals have a lot of applications. Its main application is that it is used to find out the area under the curve of a function, as shown below:
