Why does oxygen show anomalous behavior ?
- Large size, high electronegativity
- Small size, small electronegativity
- Small size, high electronegativity, absence of vacant d- orbital
- Large size high electronegativity presence of vacant d orbital
The Correct Option is C
Solution and Explanation
Top Questions on Group 16 Elements
- Choose the correct statements from the following:
A. All group 16 elements form oxides of general formula \( EO_2 \) and \( EO_3 \) where \( E = S, Se, Te, \) and Po. Both the types of oxides are acidic in nature.
B. TeO\(_2\) is an oxidising agent while SO\(_2\) is reducing in nature.
C. The reducing property decreases from H\(_2\)S to H\(_2\)Te down the group.
D. The ozone molecule contains five lone pairs of electrons.
Choose the correct answer from the options given below:- JEE Main - 2024
- Chemistry
- Group 16 Elements
- From the given list, the number of compounds with +4 oxidation state of Sulphur_____.
\(SO_3, H_2SO_3, SOCl_2, SF_4, BaSO_4, H_2S_2O_7\).- JEE Main - 2024
- Chemistry
- Group 16 Elements
- Among Group 16 elements, which one does NOT show -2 oxidation state?
- NEET (UG) - 2024
- Chemistry
- Group 16 Elements
- Given below are two statements :
Statement I: The boiling point of hydrides of Group 16 elements follow the order
H2O > H2Te > H2Se > H2S.
Statement II: On the basis of molecular mass, H2O is expected to have lower boiling point than the other members of the group but due to the presence of extensive H-bonding in H2O, it has higher boiling point.
In the light of the above statements, choose the correct answer from the options given below :- NEET (UG) - 2024
- Chemistry
- Group 16 Elements
- Cerium (IV) has a noble gas configuration. Which of the following is correct statement about it?
- JEE Main - 2022
- Chemistry
- Group 16 Elements
Questions Asked in JEE Main exam
- When a light of a given wavelength falls on a metallic surface the stopping potential for photoelectrons is \(3.2\ \text{V}\). If a second light having wavelength twice of the first light is used, the stopping potential drops to \(0.7\ \text{V}\). The wavelength of the first light is ________ m.
- JEE Main - 2026
- Photoelectric Effect
- An infinitely long straight wire carrying current $I$ is bent in a planar shape as shown in the diagram. The radius of the circular part is $r$. The magnetic field at the centre $O$ of the circular loop is :

- JEE Main - 2026
- Current electricity
- Identify the correct statements: The presence of –NO\(_2\) group in benzene ring A. activates the ring towards electrophilic substitutions. B. deactivates the ring towards electrophilic substitutions. C. activates the ring towards nucleophilic substitutions. D. deactivates the ring towards nucleophilic substitutions. Choose the correct answer from the options given below:
- JEE Main - 2026
- General Chemistry
- If the distances of the point \( (1,2,a) \) from the line \[ \frac{x-1}{1}=\frac{y}{2}=\frac{z-1}{1} \] along the lines \[ L_1:\ \frac{x-1}{3}=\frac{y-2}{4}=\frac{z-a}{b} \quad \text{and} \quad L_2:\ \frac{x-1}{1}=\frac{y-2}{4}=\frac{z-a}{c} \] are equal, then \( a+b+c \) is equal to:
- JEE Main - 2026
- Three Dimensional Geometry
Two circular discs of radius \(10\) cm each are joined at their centres by a rod, as shown in the figure. The length of the rod is \(30\) cm and its mass is \(600\) g. The mass of each disc is also \(600\) g. If the applied torque between the two discs is \(43\times10^{-7}\) dyne·cm, then the angular acceleration of the system about the given axis \(AB\) is ________ rad s\(^{-2}\).

- JEE Main - 2026
- Rotational motion
Concepts Used:
Group 16 Elements
The group 16 elements (oxygen group elements) of the periodic classification are also known as chalcogens because most of the copper ores have copper in the form of oxides and sulphides. The word chalcogen means “ore formation” which is derived from the Greek word “Chalcos” (Ore) and “gen” (formation).
There are 5 elements that come under Group 16 of the Modern Periodic Table namely:
- Oxygen (O)
- Sulphur (S)
- Selenium (Se)
- Tellurium (Te)
- Polonium (PO)
Electronic Configuration:
The general electronic configuration of the chalcogens can be written as ‘ns2np4’, where ‘n’ denotes the value of the principal quantum number corresponding to the valence shell of the element.
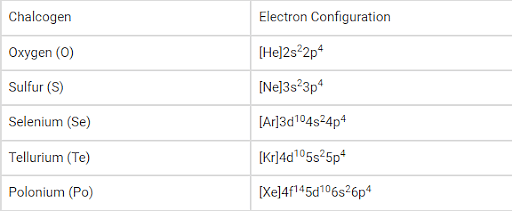
The electron configuration of the synthetic element livermorium (believed to be a chalcogen) is predicted to be [Rn]5f146d107s27p4.
Metallic Nature of the Group 16 Elements:
- Oxygen and sulfur are classified as non-metals.
- Selenium and tellurium are classified as metalloids.
- Under standard conditions, polonium exhibits metallic characteristics. However, it is important to note that polonium is a radioactive element.