What is the length of the projection of $3\hat{i}+4\hat{j}+5\hat{k}$ on the xy-plane ?
- 3
- 5
- 7
- 9
The Correct Option is B
Solution and Explanation
$\vec{a} = 3i + 4j + 5k$ make angle $\theta$ with z - axis, then it makes $90-\theta$ with xy-plane, unit vector along z-axis is k.
So, $cos\theta = \frac{\vec{a}, \hat{k}}{\left|\vec{a},\right|\cdot\left|\hat{k}\right|} = \frac{\left(3i + 4j + 5k\right).k}{|3i + 4j + 5k|}$
$= \frac{5}{5\sqrt{2}} = \frac{1}{\sqrt{2}} \Rightarrow \quad\theta = \frac{\pi}{4}$.
Hence angle with xy- plane $\frac{\pi }{2}-\frac{\pi }{4} = \frac{\pi }{4}$
projection of $\vec{a}$ on xy plane $= | \vec{a} | .cos \frac{\pi }{4}$
$= 5\sqrt{2} \times \frac{1}{\sqrt{2}} = 5.$
Top Questions on Distance of a Point from a Plane
- The square of the distance of the point \(\left( \frac{15}{7}, \frac{32}{7}, 7 \right)\) from the line \(\frac{x+1}{3} = \frac{y+3}{5} = \frac{z+5}{7}\) in the direction of the vector \(\mathbf{i} + 4\mathbf{j} + 7\mathbf{k}\) is:
- JEE Main - 2025
- Mathematics
- Distance of a Point from a Plane
- An equation of a plane parallel to the plane \(x-2y+2z-5=0\) and at a unit distance from the origin is?
- JEE Main - 2024
- Mathematics
- Distance of a Point from a Plane
For \(a, b \in \mathbb{Z}\) and \(|a - b| \leq 10\), let the angle between the plane \(P: ax + y - z = b\) and the line \(L: x - 1 = a - y = z + 1\) be \(\cos^{-1}\left(\frac{1}{3}\right)\). If the distance of the point \((6, -6, 4)\) from the plane \(P\) is \(3\sqrt{6}\), then \(a^4 + b^2\) is equal to:
- JEE Main - 2023
- Mathematics
- Distance of a Point from a Plane
Let P₁ be the plane 3x-y-7z = 11 and P₂ be the plane passing through the points (2,-1,0), (2,0,-1), and (5,1,1). If the foot of the perpendicular drawn from the point (7,4,-1) on the line of intersection of the planes P₁ and P₂ is (α, β, γ), then a + ẞ+ y is equal to
- JEE Main - 2023
- Mathematics
- Distance of a Point from a Plane
- Let \(\lambda_1, \lambda_2\) be the values of \(\lambda\) for which the points \((1, \lambda, \frac{1}{2})\) and \((-2, 0, 1)\) are at equal distance from the plane \(2x + 3y - 6z + 7 = 0\). If \(\lambda_1 > \lambda_2\), then the distance of the point \((1 - \lambda_2, \lambda_2, \lambda_1)\) from the line \(\frac{x-5}{1} = \frac{y-1}{2} = \frac{z+7}{2}\) is:
- JEE Main - 2023
- Mathematics
- Distance of a Point from a Plane
Questions Asked in VITEEE exam
- Let \( f(x) \) be defined as: \[f(x) = \begin{cases} 3 - x, & x<-3 \\ 6, & -3 \leq x \leq 3 \\ 3 + x, & x>3 \end{cases}\]
Let \( \alpha \) be the number of points of discontinuity of \( f(x) \) and \( \beta \) be the number of points where \( f(x) \) is not differentiable. Then, \( \alpha + \beta \) is:- VITEEE - 2024
- Matrices
- The area bounded by \( y - 1 = |x| \) and \( y + 1 = |x| \) is: (a) \( \frac{1}{2} \)
- VITEEE - 2024
- Conic sections
- The length of the perpendicular from the point \( (1, -2, 5) \) on the line passing through \( (1, 2, 4) \) and parallel to the line given by \( x + y - z = 0 \) and \( x - 2y + 3z - 5 = 0 \) is:
- VITEEE - 2024
- Differential equations
- If \( A \) and \( B \) are the two real values of \( k \) for which the system of equations \( x + 2y + z = 1 \), \( x + 3y + 4z = k \), \( x + 5y + 10z = k^2 \) is consistent, then \( A + B = \): (a) 3
- VITEEE - 2024
- Binomial theorem
- A and B are independent events of a random experiment if and only if:
- VITEEE - 2024
- Relations and functions
Concepts Used:
Distance of a Point from a Plane
The shortest perpendicular distance from the point to the given plane is the distance between point and plane. In simple terms, the shortest distance from a point to a plane is the length of the perpendicular parallel to the normal vector dropped from the particular point to the particular plane. Let's see the formula for the distance between point and plane.
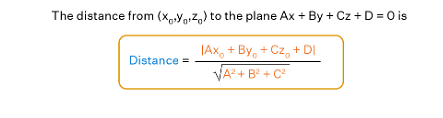
Read More: Distance Between Two Points