Two radioactive materials A and B have decay constants 25λ and 16λ respectively. If initially they have the same number of nuclei, then the ratio of the number of nuclei of B to that of A will be ‘e’ after a time \(\frac{1}{(aλ)}\). The value of a is _____.
Correct Answer: 9
Solution and Explanation
NA=N0e−25λt
NB=N0e−16λt
\(\frac{N_B}{N_A}\)=e9λt
\(t=\frac{1}{9λ}\)
Given that, ratio of the number of nuclei of B to that of A will be e after a time \(\frac{1}{9λ}\)
On comparing, a = 9
So, the answer is 9.
Top Questions on Atomic Physics
- Find the ratio of minimum to maximum wavelength of radiations emitted when an electron jumps from higher energy state into ground state of hydrogen atom.
- CBSE CLASS XII - 2025
- Physics
- Atomic Physics
- Why is the mass of a nucleus always less than the sum of the masses of its constituents, i.e. free neutrons and free protons?
- CBSE CLASS XII - 2025
- Physics
- Atomic Physics
- How is Coulomb repulsion between protons in a nucleus overcome? Explain.
- CBSE CLASS XII - 2025
- Physics
- Atomic Physics
- Two statements are given, one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer from the codes (A), (B), (C), and (D) as given below.
Two statements are given, one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer from the codes (A), (B), (C) and (D) as given below.
Assertion (A): The Balmer series in the hydrogen atom spectrum is formed when the electron jumps from a higher energy state to the ground state.
Reason (R): In Bohr's model of the hydrogen atom, the electron can jump between successive orbits only.
- CBSE CLASS XII - 2025
- Physics
- Atomic Physics
- In Bohr model of hydrogen atom, an electron is revolving in second orbit. Find the value of:
(i) angular momentum of electron,
(ii) radius of the orbit, and
(iii) kinetic energy of electron.
Take radius of first orbit of hydrogen atom as 0.5 \AA.- CBSE CLASS XII - 2025
- Physics
- Atomic Physics
Questions Asked in JEE Main exam
- Let \( [x] \) denote the greatest integer function, and let \( m \) and \( n \) respectively be the numbers of the points, where the function \( f(x) = [x] + |x - 2| \), \( -2<x<3 \), is not continuous and not differentiable. Then \( m + n \) is equal to:
- JEE Main - 2025
- Differential Equations
- Let \( f(x) = \frac{x - 5}{x^2 - 3x + 2} \). If the range of \( f(x) \) is \( (-\infty, \alpha) \cup (\beta, \infty) \), then \( \alpha^2 + \beta^2 \) equals to.
- JEE Main - 2025
- Functions
- Let \( P_n = \alpha^n + \beta^n \), \( P_{10} = 123 \), \( P_9 = 76 \), \( P_8 = 47 \), and \( P_1 = 1 \). The quadratic equation whose roots are \( \frac{1}{\alpha} \) and \( \frac{1}{\beta} \) is:
- JEE Main - 2025
- Sequences and Series
- The value of \( (\sin 70^\circ)(\cot 10^\circ \cot 70^\circ - 1) \) is:
- JEE Main - 2025
- Trigonometric Identities
Let $ P_n = \alpha^n + \beta^n $, $ n \in \mathbb{N} $. If $ P_{10} = 123,\ P_9 = 76,\ P_8 = 47 $ and $ P_1 = 1 $, then the quadratic equation having roots $ \alpha $ and $ \frac{1}{\beta} $ is:
- JEE Main - 2025
- Relations and functions
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
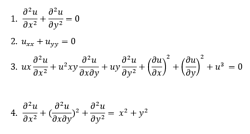
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
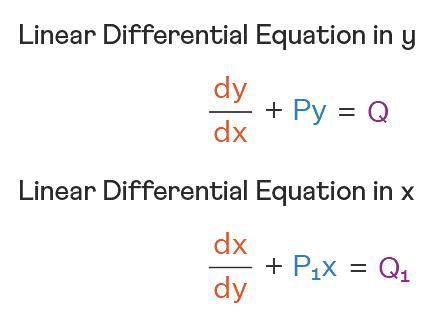
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations