Two hollow conducting spheres of radii R1 and R2 (R1 >>R2) have equal charges. The potential would be:
- More on bigger sphere
- More on smaller sphere
- Equal on both the sphere
- Dependent on the material properly of the sphere
The Correct Option is B
Solution and Explanation
When two hollow conducting spheres of radii \( R_1 \) and \( R_2 \) (where \( R_1 \gg R_2 \)) are given equal charges, we need to determine the electric potential on each sphere. The formula for the electric potential \( V \) on the surface of a charged conducting sphere is given by:
\[ V = \frac{kQ}{R} \]
where:
- \( V \) is the electric potential.
- \( k \) is Coulomb's constant.
- \( Q \) is the charge.
- \( R \) is the radius of the sphere.
Since both spheres have the same charge \( Q \), the potential \( V_1 \) on sphere 1 with radius \( R_1 \), and the potential \( V_2 \) on sphere 2 with radius \( R_2 \), are given by:
\[ V_1 = \frac{kQ}{R_1} \]
\[ V_2 = \frac{kQ}{R_2} \]
Given that \( R_1 \gg R_2 \), it follows that:
\[ V_1 = \frac{kQ}{R_1} \] will be significantly smaller than \[ V_2 = \frac{kQ}{R_2} \]
Therefore, the potential is more on the smaller sphere.
Answer: More on smaller sphere.
Top Questions on Electric Potential And Potential Difference
- A thin spherical shell is charged by some source. The potential difference between the two points C and P (in V) shown in the figure is:
(Take \(\frac{1}{4}\pi\epsilon_0 = 9 × 109\)\(\frac{1}{4\pi\epsilon_0}=9\times10^9\) SI units)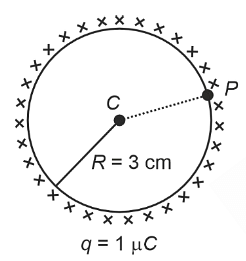
- NEET (UG) - 2024
- Physics
- Electric Potential And Potential Difference
- A charge of 10 coulomb is brought from infinity to a point \( P \) near a charged body and in this process 200 joules of work is done. Electric potential at point \( P \) is:
- JEECUP - 2024
- Physics
- Electric Potential And Potential Difference
- Two point charges \( 20 \, \mu C \) and \( -10 \, \mu C \) are separated by a distance of 1 m in air. At what point on the line joining the two charges, the electric potential is zero.
- COMEDK UGET - 2023
- Physics
- Electric Potential And Potential Difference
- Choose correct graph of electric potential for uniformly charged hollow sphere.
- JEE Main - 2023
- Physics
- Electric Potential And Potential Difference
- Electric potential at a point \( P \) due to a point charge of \( 5 \times 10^{-9} \, \text{C} \) is \( 50 \, \text{V} \). The distance of \( P \) from the point charge is:
- JEE Main - 2023
- Physics
- Electric Potential And Potential Difference
Questions Asked in NEET exam
- De-Broglie wavelength of an electron orbiting in the \(n = 2\) state of hydrogen atom is close to (Given Bohr radius = 0.052 nm):
- NEET (UG) - 2025
- de broglie hypothesis
- Which chromosome in the human genome has the highest number of genes?
- NEET (UG) - 2025
- Human genome
- In a certain camera, a combination of four similar thin convex lenses are arranged axially in contact. Then the power of the combination and the total magnification in comparison to one lens will be, respectively:
- NEET (UG) - 2025
- Images Formed By Lenses
AB is a part of an electrical circuit (see figure). The potential difference \(V_A - V_B\), at the instant when current \(i = 2\) A and is increasing at a rate of 1 amp/second is:
- NEET (UG) - 2025
- Electromagnetic Induction and Inductance
- A ball of mass 0.5 kg is dropped from a height of 10 m. The ball hits the ground and rises to a height of 1.5 m. The impulse imparted to the ball during its collision with the ground is : (Take \(g = 9.8 \, \text{m/s}^2\))
- NEET (UG) - 2025
- Collision and Impulse
Concepts Used:
Electric Potential
Electric potential is a fundamental concept in physics that helps us understand the behavior of electric charges and the effects of electric fields. It is a scalar quantity that describes the amount of electric potential energy per unit charge at a specific point in space.
The electric potential at a point is defined as the work done per unit charge in bringing a positive test charge from infinity to that point, without accelerating it. It is denoted by the symbol V and is measured in volts (V).
The electric potential is influenced by the presence of electric charges and electric fields. In the vicinity of a positive charge, the electric potential is high, indicating that there is a lot of potential energy associated with the charge. Conversely, in the vicinity of a negative charge, the electric potential is low.
The electric potential can be thought of as a "hill" or "valley" analogy, where charges are like objects that can roll downhill from higher potential (hilltops) to lower potential (valleys). The potential difference between two points, also known as voltage, determines the direction and magnitude of the electric field.
Mathematically, the electric potential can be calculated using the formula V = kQ/r, where k is the electrostatic constant, Q is the charge, and r is the distance from the charge.
Electric potential plays a crucial role in various applications, such as electric circuits, capacitors, and particle accelerators. It helps us analyze and understand the behavior of electric systems and provides a foundation for many areas of electrical engineering and physics.