Question:
Two charges \( +5 \, \mu\text{C} \) and \( +5 \, \mu\text{C} \) are placed 1 m apart. What is the electric potential at the midpoint between them? (Take \(k = 9 \times 10^9 \, \text{N.m}^2/\text{C}^2\)).
Two charges \( +5 \, \mu\text{C} \) and \( +5 \, \mu\text{C} \) are placed 1 m apart. What is the electric potential at the midpoint between them? (Take \(k = 9 \times 10^9 \, \text{N.m}^2/\text{C}^2\)).
Show Hint
For electric potential at a point due to multiple charges, sum the potentials \( V = k \frac{q}{r} \) for each charge, using consistent units (charge in C, distance in m).
Updated On: May 24, 2025
- \( 9 \times 10^4 \, \text{V} \)
- \( 1.8 \times 10^5 \, \text{V} \)
- \( 2.7 \times 10^5 \, \text{V} \)
- \( 3.6 \times 10^5 \, \text{V} \)
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
The electric potential \( V \) due to a point charge \( q \) at distance \( r \) is:
\[
V = k \frac{q}{r}
\]
The charges are \( q_1 = q_2 = 5 \times 10^{-6} \, \text{C} \), and they are 1 m apart, so the midpoint is at \( r = 0.5 \, \text{m} \) from each charge. The total potential at the midpoint is the sum of potentials due to both charges:
\[
V_{\text{total}} = V_1 + V_2 = k \frac{q_1}{r} + k \frac{q_2}{r} = \frac{k}{r} (q_1 + q_2)
\]
\[
= \frac{9 \times 10^9}{0.5} (5 \times 10^{-6} + 5 \times 10^{-6}) = 18 \times 10^9 \cdot 10 \times 10^{-6} = 18 \times 10^4 = 1.8 \times 10^5 \, \text{V}
\]
The electric potential is:
\[
\boxed{1.8 \times 10^5}
\]
Was this answer helpful?
0
0
Top Questions on Electric Potential And Potential Difference
- If a particle of mass 10 mg and charge 2 µC at rest is subjected to a uniform electric field of potential difference 160 V, then the velocity acquired by the particle is
- TS EAMCET - 2025
- Physics
- Electric Potential And Potential Difference
- A thin spherical shell is charged by some source. The potential difference between the two points C and P (in V) shown in the figure is:
(Take \(\frac{1}{4}\pi\epsilon_0 = 9 × 109\)\(\frac{1}{4\pi\epsilon_0}=9\times10^9\) SI units)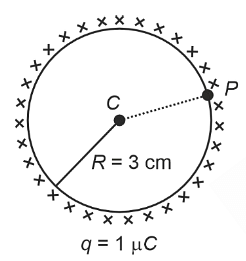
- NEET (UG) - 2024
- Physics
- Electric Potential And Potential Difference
- A charge of 10 coulomb is brought from infinity to a point \( P \) near a charged body and in this process 200 joules of work is done. Electric potential at point \( P \) is:
- JEECUP - 2024
- Physics
- Electric Potential And Potential Difference
- Two point charges \( 20 \, \mu C \) and \( -10 \, \mu C \) are separated by a distance of 1 m in air. At what point on the line joining the two charges, the electric potential is zero.
- COMEDK UGET - 2023
- Physics
- Electric Potential And Potential Difference
- Choose correct graph of electric potential for uniformly charged hollow sphere.
- JEE Main - 2023
- Physics
- Electric Potential And Potential Difference
View More Questions
Questions Asked in AP EAPCET exam
- The number of positive integers less than 10000 which contain the digit 5 at least once is
- AP EAPCET - 2025
- Permutations
- If the de Broglie wavelength of an electron is \( 2 \, \text{nm} \), then its kinetic energy is nearly (Planck's constant \( = 6.6 \times 10^{-34} \, \text{J s} \) and mass of electron \( = 9 \times 10^{-31} \, \text{kg} \))
- AP EAPCET - 2025
- Dual nature of matter
- The domain and range of a real valued function \( f(x) = \cos (x-3) \) are respectively.
- AP EAPCET - 2025
- Functions
- If a force F = (3i - 2j) N acting on a body displaces it from point (1 m, 2 m) to point (2 m, 0 m), then work done by the force is
- AP EAPCET - 2025
- work, energy and power
- Two bodies A and B of masses 1.5 kg and 3 kg are moving with velocities 20 m/s and 15 m/s respectively. If the same retarding force is applied on the two bodies, then the ratio of the distances travelled by the bodies A and B before they come to rest is
- AP EAPCET - 2025
- work, energy and power
View More Questions