The wavelength of the γ-ray emitted in
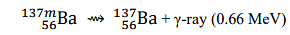
is _______ Å. (rounded off to three decimal places)
[Given: h=6.626×10 −34 J s; c=2.998×108 m s−1 ; 1 MeV=1.602×10−13 J]
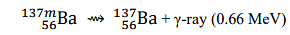
is _______ Å. (rounded off to three decimal places)
[Given: h=6.626×10 −34 J s; c=2.998×108 m s−1 ; 1 MeV=1.602×10−13 J]
Correct Answer: 0.017 - 0.021
Solution and Explanation
The wavelength \( \lambda \) of a photon can be calculated using the energy-wavelength relationship:
E = \( \frac{hc}{\lambda} \)
Where:
- E is the energy of the photon
- h is Planck’s constant \((6.626 \times 10^{-34} \, \text{J.s})\)
- c is the speed of light \((2.998 \times 10^8 \, \text{m/s})\)
- \( \lambda \) is the wavelength
We can rearrange the formula to solve for the wavelength \( \lambda \):
\( \lambda = \frac{hc}{E} \)
Given that the energy of the γ-ray is 0.66 MeV, we first need to convert this to joules:
\(E = 0.66 \, \text{MeV} \times 1.602 \times 10^{-13} \, \text{J/MeV} = 1.0573 \times 10^{-13} \, \text{J}\)
Now, substitute the values into the equation for \( \lambda \):
\(\lambda = \frac{(6.626 \times 10^{-34} \, \text{J.s})(2.998 \times 10^8 \, \text{m/s})}{1.0573 \times 10^{-13} \, \text{J}}\)
\(\lambda = 0.021 \, \text{Å}\)
Thus, the wavelength of the γ-ray is 0.021 Å (rounded to three decimal places).
Top Questions on Spectroscopy
The UV-visible spectrum of [Ni(en)\(_3\)]\(^{2+}\) (en = ethylenediamine) shows absorbance maxima at 11200 cm\(^{-1}\), 18350 cm\(^{-1}\), and 29000 cm\(^{-1}\).

[Given: Atomic number of Ni = 28] The correct match(es) between absorbance maximum and electronic transition is/are
- GATE CY - 2025
- Chemistry
- Spectroscopy
Compound K displayed a strong band at 1680 cm−1 in its IR spectrum. Its 1H-NMR spectral data are as follows:
δ (ppm):
7.30 (d, J = 7.2 Hz, 2H)
6.80 (d, J = 7.2 Hz, 2H)
3.80 (septet, J = 7.0 Hz, 1H)
2.20 (s, 3H)
1.90 (d, J = 7.0 Hz, 6H)The correct structure of compound K is:
- GATE CY - 2025
- Chemistry
- Spectroscopy
The 1H NMR spectrum of the given iridium complex at room temperature gave a single signal at 2.6 ppm, and its 31P NMR spectrum gave a single signal at 23.0 ppm. When the spectra were recorded at lower temperatures, both these signals split into a complex pattern. The intra-molecular dynamic processes shown by this molecule are:

- GATE CY - 2025
- Chemistry
- Spectroscopy
- The total number of hyperfine lines expected in the EPR spectrum of •CH2OH (radical) is ___________ (in integer).
- GATE CY - 2025
- Chemistry
- Spectroscopy
- Compound(s) that show(s) an intense peak at \( m/z = 120 \) in the EI mass spectrum is/are:
- GATE CY - 2025
- Chemistry
- Spectroscopy
Questions Asked in IIT JAM CY exam
One mole of a monoatomic ideal gas starting from state A, goes through B and C to state D, as shown in the figure. Total change in entropy (in J K\(^{-1}\)) during this process is ...............

- IIT JAM CY - 2025
- Thermodynamics
The number of chiral carbon centers in the following molecule is ...............

- IIT JAM CY - 2025
- General Chemistry
- Consider the following matrices A and B.
\[ A = \begin{pmatrix} 1 & 2 & 0 & 0 \\ 3 & 4 & 0 & 0 \\ 0 & 5 & 5 & 0 \\ 0 & 0 & 6 & 7 \\ 0 & 0 & 8 & 9 \end{pmatrix} \quad \text{and} \quad B = \begin{pmatrix} 10 & 11 & 0 & 0 & 0 \\ 12 & 13 & 0 & 0 & 0 \\ 0 & 0 & 4 & 0 & 0 \\ 0 & 0 & 15 & 16 & 0 \\ 0 & 0 & 17 & 18 & 0 \end{pmatrix} \]
If \( C = AB \), the sum of the diagonal elements of \( C \) is ..............
- IIT JAM CY - 2025
- General Chemistry
A tube fitted with a semipermeable membrane is dipped into 0.001 M NaCl solution at 300 K as shown in the figure. Assume density of the solvent and solution are the same. At equilibrium, the height of the liquid column \( h \) (in cm) is .........

- IIT JAM CY - 2025
- General Chemistry
An electron at rest is accelerated through 10 kV potential. The de Broglie wavelength (in A) of the electron is .............
- IIT JAM CY - 2025
- General Chemistry