The value of the definite integral $\int\limits_{0}^{1}\frac{x\,dx}{x^3+16}$ lies in the interval [a, h], The smallest such interval is
- $\left[0,\frac{1}{17}\right]$
- $[0,1]$
- $\left[0,\frac{1}{27}\right]$
- none of these,
The Correct Option is A
Solution and Explanation
Top Questions on Definite Integral
- Evaluate the definite integral: \( \int_{-2}^{2} |x^2 - x - 2| \, dx \)
- MHT CET - 2025
- Mathematics
- Definite Integral
The value \( 9 \int_{0}^{9} \left\lfloor \frac{10x}{x+1} \right\rfloor \, dx \), where \( \left\lfloor t \right\rfloor \) denotes the greatest integer less than or equal to \( t \), is ________.
- JEE Main - 2024
- Mathematics
- Definite Integral
- The value of \(\lim_{{n \to \infty}} \sum_{{k=1}}^{n} \frac{n^3}{{(n^2 + k^2)(n^2 + 3k^2)}}\) is
- JEE Main - 2024
- Mathematics
- Definite Integral
If the value of the integral
\[ \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left( \frac{x^2 \cos x}{1 + \pi^x} + \frac{1 + \sin^2 x}{1 + e^{\sin^x 2023}} \right) dx = \frac{\pi}{4} (\pi + a) - 2, \]
then the value of \(a\) is:
- JEE Main - 2024
- Mathematics
- Definite Integral
- For \( x \in \left( -\frac{\pi}{2}, \frac{\pi}{2} \right) \), if\[y(x) = \int \frac{\csc x + \sin x}{\csc x \sec x + \tan x \sin^2 x} \, dx\]and\[\lim_{x \to -\frac{\pi}{2}} y(x) = 0\]then \( y\left(\frac{\pi}{4}\right) \) is equal to
- JEE Main - 2024
- Mathematics
- Definite Integral
Concepts Used:
Definite Integral
Definite integral is an operation on functions which approximates the sum of the values (of the function) weighted by the length (or measure) of the intervals for which the function takes that value.
Definite integrals - Important Formulae Handbook
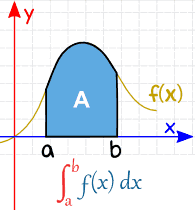
A real valued function being evaluated (integrated) over the closed interval [a, b] is written as :
\(\int_{a}^{b}f(x)dx\)
Definite integrals have a lot of applications. Its main application is that it is used to find out the area under the curve of a function, as shown below: