Question

The unit cell of a two-dimensional square lattice with lattice parameter a is indicated by the dashed lines as shown below:

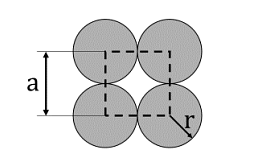
The percentage (%) area occupied by the grey circles (of radius r) inside the unit cell is _______. (rounded off to the nearest integer)

Answer 1

Correct Answer: 77 - 79

In a two-dimensional square lattice, the unit cell is a square with side length a. The four grey circles inside the unit cell have a radius r. The total area occupied by the grey circles is the combined area of the four circles.

The area of one circle is given by the formula:

A_circle = \( \pi r^2 \)

Since there are four circles in the unit cell, the total area occupied by the circles is:

A_total = 4 · \( \pi r^2 \)

The area of the square unit cell is:

A_unitcell = \( a^2 \)

Since the distance between the centers of adjacent circles is a, the relationship between a and r is:

a = 2r

Therefore, the area occupied by the grey circles as a percentage of the total unit cell area is:

Percentage occupied = \( \frac{A_{total}}{A_{unitcell}} \) × 100 = \( \frac{4 \cdot \pi r^2}{(2r)^2} \) × 100

Simplifying this:

Percentage occupied = \( \frac{4 \cdot \pi r^2}{4r^2} \) × 100 = \( \pi \) × 100 ≈ 77%

Thus, the percentage area occupied by the grey circles is 77%.