Question:
The length of a metal wire is l When the tension in it is T and is l when the tension is T. The natural length of the wire is
The length of a metal wire is l When the tension in it is T and is l when the tension is T. The natural length of the wire is
Updated On: Jun 7, 2022
- $\frac{l_{1}+l_{2}}{2}$
- $\sqrt{l_{1}l_{2}}$
- $\frac{l_{1}T_{2}-l_{2}T_{1}}{T_{2}-T_{1}}$
- $\frac{l_{1}T_{2}+l_{2}T_{1}}{T_{2}-T_{1}}$
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
Let the natural length of the wire will be l
Young?s modulus $=\frac{T}{A}\times\frac{l_{0}}{\Delta l_{0}}$
First case:
$y=\frac{T_{1}}{A}=\frac{l_{0}}{\left(l_{1}-l_{0}\right)}$
Second case:
$Y=\frac{T_{2}}{A}=\frac{l_{0}}{\left(l_{2}-l_{0}\right)}$
So, $\frac{T_{1}}{A}\times\frac{l_{0}}{\left(l_{2}-l_{0}\right)}=\frac{T_{2}}{A} \frac{l_{0}}{\left(l_{2}-l_{0}\right)}$
$\Rightarrow T_{1}\left(l_{2}-l_{0}\right)=T_{2}\left(l_{1}-l_{0}\right)$
$\Rightarrow T_{1} l_{2}-T_{1} l_{0}=T_{2}l_{1}-T_{2}l_{0}$
$\Rightarrow l_{0}=\frac{\left(T_{2}l_{1}-T_{2}l_{2}\right)}{\left(T_{2}-T_{1}\right)}$
Young?s modulus $=\frac{T}{A}\times\frac{l_{0}}{\Delta l_{0}}$
First case:
$y=\frac{T_{1}}{A}=\frac{l_{0}}{\left(l_{1}-l_{0}\right)}$
Second case:
$Y=\frac{T_{2}}{A}=\frac{l_{0}}{\left(l_{2}-l_{0}\right)}$
So, $\frac{T_{1}}{A}\times\frac{l_{0}}{\left(l_{2}-l_{0}\right)}=\frac{T_{2}}{A} \frac{l_{0}}{\left(l_{2}-l_{0}\right)}$
$\Rightarrow T_{1}\left(l_{2}-l_{0}\right)=T_{2}\left(l_{1}-l_{0}\right)$
$\Rightarrow T_{1} l_{2}-T_{1} l_{0}=T_{2}l_{1}-T_{2}l_{0}$
$\Rightarrow l_{0}=\frac{\left(T_{2}l_{1}-T_{2}l_{2}\right)}{\left(T_{2}-T_{1}\right)}$
Was this answer helpful?
0
0
Top Questions on elastic moduli
- The slope of the stress-strain curve in the elastic deformation region is
- JKCET - 2024
- Physics
- elastic moduli
- The law which states that within elastic limits strain produced is proportional to the stress producing it is known as
- JKCET - 2024
- Physics
- elastic moduli
- A wire of length L and radius r is clamped rigidly at one end. When the other end of the wire is pulled by a force F, its length increases by 5 cm. Another wire of the same material of length 4L and radius 4r is pulled by a force 4F under same conditions. The increase in length of this wire is ___ cm.
- JEE Main - 2022
- Physics
- elastic moduli
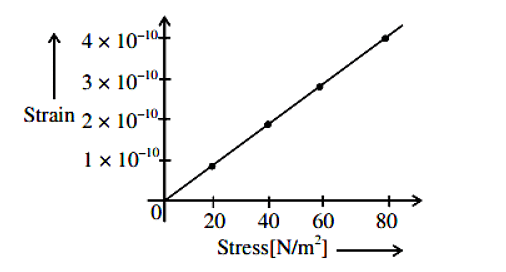
The elastic behavior of material for linear stress and linear strain, is shown in the figure. The energy density for a linear strain of 5×10–4 is ____ kJ/m3. Assume that material is elastic up to the linear strain of 5×10–4
- JEE Main - 2022
- Physics
- elastic moduli
- If the length of a wire is made double and radius is halved of its respective values. Then, the Young’s modulus of the material of the wire will :
- JEE Main - 2022
- Physics
- elastic moduli
View More Questions
Questions Asked in JIPMER exam
- Binomial nomenclature was first introduced by
- JIPMER - 2015
- KCET - 2022
- Diversity In The Living World
- $2,4-DNP $ test can be used to identify :
- JIPMER - 2021
- Chemical Reactions
- A convex lens $'A'$ of focal length $20\, cm$ and a concave lens $'B'$ of focal length $5\, cm$ are kept along the same axis with a distance $'d'$ between them. If a parallel beam of light falling on $'A'$ leaves $'B'$ as a parallel beam, then the distance $'d'$ in cm will be :
- JIPMER - 2021
- Spherical Mirrors
- A bacterial flagellum is composed of
- JIPMER - 2021
- Prokaryotic Cells
- How many moles of acidified $K_2Cr_2O_7$ is required to liberate $6$ moles of $I_2$ from an aqueous solution of $I^-$ ?
- JIPMER - 2020
- Mole concept and Molar Masses
View More Questions