The identity element in the group $M = \left\{
\begin{bmatrix}
x & x \\
x & x\\
\end{bmatrix} | x \ \in \ R, x \neq 0 \right\}$ with respect to matrix multiplication is
- $\begin{bmatrix}1 & 1 \\1 & 1\\\end{bmatrix} $
- $\frac {1} {2} \begin{bmatrix} 1 & 1 \\ 1 & 1\\ \end{bmatrix} $
- $\begin{bmatrix}1 & 0 \\0 & 1\\ \end{bmatrix} $
- $\begin{bmatrix}0 & 1 \\1 & 0\\\end{bmatrix} $
The Correct Option is B
Solution and Explanation
Let $P$ be the identity element in the group
i.e. $P=\begin{bmatrix}\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2}\end{bmatrix}=\frac{1}{2}\begin{bmatrix}1 & 1 \\ 1 & 1\end{bmatrix}$
$P$ is obtained by putting $x=\frac{1}{2}$
$\therefore \, M P=\begin{bmatrix}x & x \\ x & x\end{bmatrix}\begin{bmatrix}\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2}\end{bmatrix}=M$
and $PM=\begin{bmatrix}\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2}\end{bmatrix}\begin{bmatrix}x & x \\ x & x\end{bmatrix}=M$
$\therefore\, M P=M=P M$
Top Questions on Transpose of a Matrix
If the matrix $ A $ is such that $ A \begin{pmatrix} -1 & 2 \\ 3 & 1 \end{pmatrix} = \begin{pmatrix} -4 & 1 \\ 7 & 7 \end{pmatrix} \text{ then } A \text{ is equal to} $
- COMEDK UGET - 2024
- Mathematics
- Transpose of a Matrix
If $A = \begin{bmatrix} 5a & -b \\ 3 & 2 \end{bmatrix} \quad \text{and} \quad A \, \text{adj} \, A = A A^t, \quad \text{then} \, 5a + b \, \text{is equal to}$
- COMEDK UGET - 2024
- Mathematics
- Transpose of a Matrix
If $3A + 4B^{t} = \left( \begin{array}{cc} 7 & -10 \\ 0 & 6 \end{array} \right) $ and $ 2B - 3A^{t} = \left( \begin{array}{cc} -1 & 18 \\ 4 & -6 \\ -5 & -7 \end{array} \right) $, then find $ (5B)^{t}$:
- COMEDK UGET - 2024
- Mathematics
- Transpose of a Matrix
- If \( A = \begin{bmatrix} 0 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1 \end{bmatrix} \), then \( A^{-1} \) is:
- MHT CET - 2024
- Mathematics
- Transpose of a Matrix
- If \[ B = \begin{bmatrix} 3 & \alpha & -1 \\ 1 & 3 & 1 \\ -1 & 1 & 3 \end{bmatrix} \] is the adjoint of a 3x3 matrix \( A \) and \( |A| = 4 \), then \( \alpha \) is equal to:
- MHT CET - 2024
- Mathematics
- Transpose of a Matrix
Questions Asked in KCET exam
- If the number of terms in the binomial expansion of \((2x + 3)^n\) is 22, then the value of \(n\) is:
- KCET - 2025
- Binomial theorem
- Ethyl alcohol is heated with concentrated sulphuric acid at 413 K (140°C). The major product formed is
- KCET - 2025
- Organic Chemistry
- A body of mass 0.25 kg travels along a straight line from \( x = 0 \) to \( x = 2 \, \text{m} \) with a speed \( v = k x^2 \) where \( k = 2 \, \text{m}^{-1} \). The work done by the net force during this displacement is
- KCET - 2025
- Elastic and inelastic collisions
- A square loop of side 2 m lies in the Y-Z plane in a region having a magnetic field \(\mathbf{B} = (5 \hat{i} - 3 \hat{j} - 4 \hat{k}) \, \text{T}\). The magnitude of magnetic flux through the square loop is
- KCET - 2025
- Magnetic Field
- A random experiment has five outcomes \(w_1, w_2, w_3, w_4, w_5\). The probabilities of the occurrence of the outcomes \(w_1, w_2, w_4, w_5\) are respectively \( \frac{1}{6}, a, b, \frac{1}{12} \) such that \(12a + 12b - 1 = 0\). Then the probabilities of occurrence of the outcome \(w_3\) is:
- KCET - 2025
- Probability
Concepts Used:
Transpose of a Matrix
The matrix acquired by interchanging the rows and columns of the parent matrix is called the Transpose matrix. The transpose matrix is also defined as - “A Matrix which is formed by transposing all the rows of a given matrix into columns and vice-versa.”
The transpose matrix of A is represented by A’. It can be better understood by the given example:

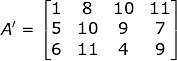
Now, in Matrix A, the number of rows was 4 and the number of columns was 3 but, on taking the transpose of A we acquired A’ having 3 rows and 4 columns. Consequently, the vertical Matrix gets converted into Horizontal Matrix.
Hence, we can say if the matrix before transposing was a vertical matrix, it will be transposed to a horizontal matrix and vice-versa.
Read More: Transpose of a Matrix