Question:
The Henry’s law constant of CO$_2$ is $3.4 \times 10^{-2}$ M/atm at 25$^\circ$C.
Dissolved CO$_2$ undergoes:
CO$_2 \cdot$H$_2$O $\rightleftharpoons$ H$^+$ + HCO$_3^-$ ($K_1 = 4.3 \times 10^{-7}$ M)
HCO$_3^- \rightleftharpoons$ H$^+$ + CO$_3^{2-}$ ($K_2 = 4.7 \times 10^{-11}$ M)
If ambient CO$_2$ concentration is 300 ppm, the total dissolved CO$_2$ (in $\mu$M, rounded off to one decimal place) is __________.
The Henry’s law constant of CO$_2$ is $3.4 \times 10^{-2}$ M/atm at 25$^\circ$C.
Dissolved CO$_2$ undergoes:
CO$_2 \cdot$H$_2$O $\rightleftharpoons$ H$^+$ + HCO$_3^-$ ($K_1 = 4.3 \times 10^{-7}$ M)
HCO$_3^- \rightleftharpoons$ H$^+$ + CO$_3^{2-}$ ($K_2 = 4.7 \times 10^{-11}$ M)
If ambient CO$_2$ concentration is 300 ppm, the total dissolved CO$_2$ (in $\mu$M, rounded off to one decimal place) is __________.
Dissolved CO$_2$ undergoes:
CO$_2 \cdot$H$_2$O $\rightleftharpoons$ H$^+$ + HCO$_3^-$ ($K_1 = 4.3 \times 10^{-7}$ M)
HCO$_3^- \rightleftharpoons$ H$^+$ + CO$_3^{2-}$ ($K_2 = 4.7 \times 10^{-11}$ M)
If ambient CO$_2$ concentration is 300 ppm, the total dissolved CO$_2$ (in $\mu$M, rounded off to one decimal place) is __________.
Show Hint
Total dissolved CO$_2$ = molecular CO$_2$ + bicarbonate + carbonate; bicarbonate dominates at neutral pH.
Updated On: Dec 17, 2025
Hide Solution
Verified By Collegedunia
Correct Answer: 54
Solution and Explanation
Ambient CO$_2$ partial pressure:
\[ P_{CO_2} = 300\ \text{ppm} = 300 \times 10^{-6}\ \text{atm} = 3 \times 10^{-4}\ \text{atm}. \]
Dissolved molecular CO$_2$:
\[ [\text{CO}_2(\text{aq})] = H\, P_{CO_2} = (3.4 \times 10^{-2})(3 \times 10^{-4}) = 1.02 \times 10^{-5}\ \text{M}. \]
At neutral pH, \([H^+] = 10^{-7}\) M.
First dissociation:
\[ \frac{[\text{HCO}_3^-]}{[\text{CO}_2]} = \frac{K_1}{[H^+]} = \frac{4.3\times 10^{-7}}{10^{-7}} = 4.3. \]
Second dissociation is negligible (very tiny):
\[ \frac{[\text{CO}_3^{2-}]}{[\text{HCO}_3^-]} = \frac{K_2}{[H^+]} = 4.7\times 10^{-4}. \]
Thus total dissolved inorganic carbon:
\[ [\text{Total}] = [\text{CO}_2] (1 + 4.3 + 4.3 \times 4.7\times 10^{-4}). \]
Compute:
\[ 1 + 4.3 + 0.002 = 5.302. \]
\[ [\text{Total}] = 1.02\times10^{-5} \times 5.302 = 5.41\times 10^{-5}\,\text{M}. \]
Convert to $\mu$M:
\[ 5.41\times10^{-5}\,\text{M} = 54.1\ \mu\text{M}. \]
Thus the answer is:
\[ \boxed{54.1\ \mu\text{M}} \quad (\text{acceptable range: } 54.0\text{–}54.2) \]
\[ P_{CO_2} = 300\ \text{ppm} = 300 \times 10^{-6}\ \text{atm} = 3 \times 10^{-4}\ \text{atm}. \]
Dissolved molecular CO$_2$:
\[ [\text{CO}_2(\text{aq})] = H\, P_{CO_2} = (3.4 \times 10^{-2})(3 \times 10^{-4}) = 1.02 \times 10^{-5}\ \text{M}. \]
At neutral pH, \([H^+] = 10^{-7}\) M.
First dissociation:
\[ \frac{[\text{HCO}_3^-]}{[\text{CO}_2]} = \frac{K_1}{[H^+]} = \frac{4.3\times 10^{-7}}{10^{-7}} = 4.3. \]
Second dissociation is negligible (very tiny):
\[ \frac{[\text{CO}_3^{2-}]}{[\text{HCO}_3^-]} = \frac{K_2}{[H^+]} = 4.7\times 10^{-4}. \]
Thus total dissolved inorganic carbon:
\[ [\text{Total}] = [\text{CO}_2] (1 + 4.3 + 4.3 \times 4.7\times 10^{-4}). \]
Compute:
\[ 1 + 4.3 + 0.002 = 5.302. \]
\[ [\text{Total}] = 1.02\times10^{-5} \times 5.302 = 5.41\times 10^{-5}\,\text{M}. \]
Convert to $\mu$M:
\[ 5.41\times10^{-5}\,\text{M} = 54.1\ \mu\text{M}. \]
Thus the answer is:
\[ \boxed{54.1\ \mu\text{M}} \quad (\text{acceptable range: } 54.0\text{–}54.2) \]
Was this answer helpful?
0
0
Top Questions on Chemical equilibria
- The ratio of osmotic pressures of aqueous solutions of 0.01 M BaCl2 to 0.005 M NaCl is
[Given: Both compounds dissociate completely in water]- IIT JAM CY - 2024
- Physical Chemistry
- Chemical equilibria
- A 1.0 L solution is prepared by dissolving 2.0 g of benzoic acid and 4.0 g of sodium benzoate in water. The pH of the resulting solution is _______. (rounded off to one decimal place)
Given: Molar mass of benzoic acid is 122 g mol−1
Molar mass of sodium benzoate is 144 g mol−1
p𝐾a of benzoic acid is 4.2- IIT JAM CY - 2024
- Physical Chemistry
- Chemical equilibria
- 0.1 M aqueous solution of a weak monobasic acid has pH 2.0. The pKa of the monobasic acid is _______. (rounded off to one decimal place)
- IIT JAM CY - 2024
- Physical Chemistry
- Chemical equilibria
- Consider the exothermic chemical reaction O2(𝑔)+2H2(𝑔) ⇌ 2H2O(𝑔) at equilibrium in a closed container. The correct statement(s) is/are
- IIT JAM CY - 2024
- Physical Chemistry
- Chemical equilibria
- The isoelectric point of glutamic acid is ______.
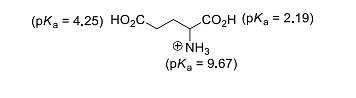
(round off to two decimal places)- IIT JAM CY - 2023
- Physical Chemistry
- Chemical equilibria
View More Questions
Questions Asked in GATE ES exam
- Water from a hand pump located near a landfill has 1 mg/L arsenic (oral carcinogenic potency factor = 1.75 (kg-day)/mg). A person who lives nearby drinks 2 L/day of water from this hand pump for 10 years. Assume a body weight of 70 kg and an average life duration of 70 years. The chances of this person getting an excess risk of cancer is ________ $\times 10^{-3$ (rounded off to three decimal places).}
- GATE ES - 2025
- Hydrology
- An industry releases three greenhouse gases (GHGs), CO2 (5 kg/day), CH4 (0.5 kg/day), and N2O (0.1 kg/day). The industry flares the CH4 before it is released to the atmosphere. The Global Warming Potential (GWP) are as follows: CO2 = 1, CH4 = 21, N2O = 310. The annual GWP of GHGs released from the industry is ________ kg CO2 equivalent (rounded off to the nearest integer).
- GATE ES - 2025
- Greenhouse Effect
- A solid waste of composition \( C_{60}H_{135}O_{50}N_5 \) is to be composted aerobically in a closed vessel mechanical composting facility. Given: all ammonia generated escapes the facility; air contains 23% of Oxygen by weight; 100% excess air requirement for the closed vessel composting facility. The atomic weights: C – 12, H – 1, O – 16, N – 14. The actual air required for composting is:
- GATE ES - 2025
- Waste Management
A particle dispersoid has 1510 spherical particles of uniform density. An air purifier is proposed to be used to remove these particles. The diameter-specific number of particles in the dispersoid, along with the number removal efficiency of the proposed purifier is shown in the following table:

The overall mass removal efficiency of the proposed purifier is ________% (rounded off to one decimal place).- GATE ES - 2025
- Hydrology
- A boiler burns coal at a rate of 1 kg/s. If the coal has 3% sulfur content, assuming that there is no sulfur in ash, SO2 emitted is ________ kg/day. (rounded off to nearest integer)
- GATE ES - 2025
- Indoor air pollution
View More Questions