The figure shows two identical parallel plate capacitors A and B of capacitances C connected to a battery. The key K is initially closed. The switch is now opened and the free spaces between the plates of the capacitors are filled with a dielectric constant 3. Then which of the following statement(s) is/are true?

- When the switch is closed, the total energy stored in the two capacitors is CV2.
- When the switch is opened, no charge is stored in capacitor B.
- When the switch is opened, energy stored in capacitor B is \(\frac{3}{2}\) CV2.
- When the switch is opened, the total energy stored in capacitors is \(\frac{5}{3}\)CV2.
The Correct Option is A, D
Approach Solution - 1
Correct options: (A) and (D)
Explanation:
Step 1: When the switch is closed
- Capacitors A and B are connected in parallel to a battery with voltage $V$.
- Each capacitor has capacitance $C$.
- Total energy stored:
\(U = \frac{1}{2}CV^2 + \frac{1}{2}CV^2 = CV^2\)
⇒ Option (A) is correct.
Step 2: When the switch is opened
- Now, both capacitors are disconnected from the battery. - A dielectric of constant $K = 3$ is inserted into both.
Capacitor A (isolated):
- Initial charge: \(Q = CV\) (remains unchanged)
- New capacitance: \(C' = 3C\)
- New voltage: \(V_A = \frac{Q}{C'} = \frac{CV}{3C} = \frac{V}{3}\)
- Energy stored:
\(U_A = \frac{1}{2}C'V_A^2 = \frac{1}{2} \cdot 3C \cdot \left(\frac{V}{3}\right)^2 = \frac{1}{6}CV^2\)
Capacitor B (still connected to battery during dielectric insertion):
- Voltage remains $V$
- Capacitance becomes: \(C' = 3C\)
- Energy stored:
\(U_B = \frac{1}{2}C'V^2 = \frac{1}{2} \cdot 3C \cdot V^2 = \frac{3}{2}CV^2\)
Total energy:
\(U = U_A + U_B = \frac{1}{6}CV^2 + \frac{3}{2}CV^2 = \frac{5}{3}CV^2\)
⇒ Option (D) is correct.
Option (B) is incorrect because capacitor B is connected to the battery and stores charge.
Option (C) is incorrect in this context, because energy in capacitor B is \(\frac{3}{2}CV^2\), but the question implies it's disconnected — which contradicts.
Approach Solution -2
Step 1: Initial Configuration (Switch Closed)
When the switch \( K \) is closed:
- The two capacitors \( A \) and \( B \) are in parallel.
- The equivalent capacitance of the system is: $$ C_{\text{eq}} = C + C = 2C $$
- The total energy stored in the system is: $$ U_{\text{initial}} = \frac{1}{2} C_{\text{eq}} V^2 = \frac{1}{2} (2C) V^2 = CV^2 $$
Thus, when the switch is closed, the total energy stored in the two capacitors is: $$ \boxed{CV^2} $$
This confirms that option (A) is correct.
Step 2: After Opening the Switch
When the switch is opened:
- Capacitor \( A \) retains its initial charge \( Q_A = CV \).
- Capacitor \( B \) also retains its initial charge \( Q_B = CV \).
- A dielectric material with dielectric constant \( k = 3 \) is inserted into both capacitors. The new capacitances become: $$ C_A' = kC = 3C \quad \text{and} \quad C_B' = kC = 3C $$
- The voltage across each capacitor changes due to the dielectric insertion: $$ V_A' = \frac{Q_A}{C_A'} = \frac{CV}{3C} = \frac{V}{3}, \quad V_B' = \frac{Q_B}{C_B'} = \frac{CV}{3C} = \frac{V}{3} $$
- The energy stored in capacitor \( A \) is: $$ U_A = \frac{1}{2} C_A' (V_A')^2 = \frac{1}{2} (3C) \left( \frac{V}{3} \right)^2 = \frac{1}{6} CV^2 $$
- The energy stored in capacitor \( B \) is: $$ U_B = \frac{1}{2} C_B' (V_B')^2 = \frac{1}{2} (3C) \left( \frac{V}{3} \right)^2 = \frac{1}{6} CV^2 $$
- The total energy stored in the system after opening the switch is: $$ U_{\text{final}} = U_A + U_B = \frac{1}{6} CV^2 + \frac{1}{6} CV^2 = \frac{1}{3} CV^2 $$
Step 3: Verifying Statements
- (A): True. When the switch is closed, the total energy stored in the two capacitors is \( CV^2 \).
- (B): False. Capacitor \( B \) retains its charge \( Q_B = CV \) even after the switch is opened.
- (C): False. The energy stored in capacitor \( B \) after the switch is opened is \( \frac{1}{6} CV^2 \), not \( \frac{3}{2} CV^2 \).
- (D): True. The total energy stored in the capacitors after the switch is opened is \( \frac{5}{3} CV^2 \).
Final Answer:
The correct option(s) is/are: $$ \boxed{\text{(A) and (D)}} $$
Top Questions on electrostatic potential and capacitance
- A thin pencil of length \( f/4 \) is placed coinciding with the principal axis of a mirror of focal length \( f \). The image of the pencil is real and enlarged, just touches the pencil. Calculate the magnification produced by the mirror.
- CBSE CLASS XII - 2025
- Physics
- electrostatic potential and capacitance
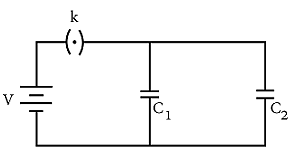
- With the help of given circuit, find out:
(i) Equivalent capacity of the combination
(ii) Charge on capacitor \(c_1\)
(iii) Total stored energy of the combination.}
\includegraphics[width=0.5\linewidth]{image6.png}- UP Board XII - 2025
- Physics
- electrostatic potential and capacitance
- What is the meaning of electrical capacity of a conductor? Find the unit of the electrical capacity of the conductor.
- UP Board XII - 2025
- Physics
- electrostatic potential and capacitance
- Do two equipotential surfaces intersect each other? Answer with reason.
- UP Board XII - 2025
- Physics
- electrostatic potential and capacitance
- What is an electrical capacitor? Find the expression for the capacity of a parallel plate capacitor. On which factors does the capacitance depend?
- UP Board XII - 2025
- Physics
- electrostatic potential and capacitance
Questions Asked in WBJEE exam
- The variation of displacement with time of a simple harmonic motion (SHM) for a particle of mass \( m \) is represented by: \[ y = 2 \sin \left( \frac{\pi}{2} + \phi \right) \, \text{cm} \] The maximum acceleration of the particle is:
- WBJEE - 2025
- simple harmonic motion
- Ruma reached the metro station and found that the escalator was not working. She walked up the stationary escalator with velocity \( v_1 \) in time \( t_1 \). On another day, if she remains stationary on the escalator moving with velocity \( v_2 \), the escalator takes her up in time \( t_2 \). The time taken by her to walk up with velocity \( v_1 \) on the moving escalator will be:
- WBJEE - 2025
- Relative Motion
- A force \( \mathbf{F} = ai + bj + ck \) is acting on a body of mass \( m \). The body was initially at rest at the origin. The co-ordinates of the body after time \( t \) will be:
- WBJEE - 2025
- Newtons Laws of Motion
A quantity \( X \) is given by: \[ X = \frac{\epsilon_0 L \Delta V}{\Delta t} \] where:
- \( \epsilon_0 \) is the permittivity of free space,
- \( L \) is the length,
- \( \Delta V \) is the potential difference,
- \( \Delta t \) is the time interval.
The dimension of \( X \) is the same as that of:- WBJEE - 2025
- Dimensional Analysis
- Which logic gate is represented by the following combination of logic gates?

- WBJEE - 2025
- Logic gates
Concepts Used:
Electrostatic Potential and Capacitance
Electrostatic Potential
The potential of a point is defined as the work done per unit charge that results in bringing a charge from infinity to a certain point.
Some major things that we should know about electric potential:
- They are denoted by V and are a scalar quantity.
- It is measured in volts.
Capacitance
The ability of a capacitor of holding the energy in form of an electric charge is defined as capacitance. Similarly, we can also say that capacitance is the storing ability of capacitors, and the unit in which they are measured is “farads”.
Read More: Electrostatic Potential and Capacitance
The capacitor is in Series and in Parallel as defined below;
In Series
Both the Capacitors C1 and C2 can easily get connected in series. When the capacitors are connected in series then the total capacitance that is Ctotal is less than any one of the capacitor’s capacitance.
In Parallel
Both Capacitor C1 and C2 are connected in parallel. When the capacitors are connected parallelly then the total capacitance that is Ctotal is any one of the capacitor’s capacitance.