The area enclosed by y2 = 8x and y = √2x that lies outside the triangle formed by \(y=√2x,x=1,y=2√2\), is equal to
The area enclosed by y2 = 8x and y = √2x that lies outside the triangle formed by \(y=√2x,x=1,y=2√2\), is equal to
- \(\frac{16\sqrt2}{6}\)
- \(\frac{11\sqrt2}{6}\)
- \(\frac{13\sqrt2}{6}\)
- \(\frac{5\sqrt2}{6}\)
The Correct Option is C
Solution and Explanation
The correct option is(C): \(\frac{13\sqrt2}{6}\)
\(=\frac{\sqrt2}{6}(48-32-3)=\frac{13\sqrt2}{6}\)
Top Questions on types of differential equations
- If \( (2,3) \) is the focus and \( x - y + 3 = 0 \) is the directrix of a parabola, then the equation of the tangent drawn at the vertex of the parabola is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- If \( m_1 \) and \( m_2 \) are the slopes of the direct common tangents drawn to the circles \[ x^2 + y^2 - 2x - 8y + 8 = 0 \quad \text{and} \quad x^2 + y^2 - 8x + 15 = 0 \] then \( m_1 + m_2 \) is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- The equation of the common tangent to the parabola \(y^2 = 8x\) and the circle \(x^2 + y^2 = 2\) is \(ax + by + 2 = 0\). If \(-\frac{a}{b}>0\), then \(3a^2 + 2b + 1 =\)
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- The axis of a parabola is parallel to Y-axis. If this parabola passes through the points \( (1,0), (0,2), (-1,-1) \) and its equation is \( ax^2 + bx + cy + d = 0 \), then \( \frac{ad}{bc} \) is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
Consider the parabola \(25[(x-2)^2 + (y+5)^2] = (3x+4y-1)^2\), match the characteristic of this parabola given in List-I with its corresponding item in List-II.
- TS EAMCET - 2024
- Mathematics
- types of differential equations
Questions Asked in JEE Main exam
If the domain of the function \( f(x) = \frac{1}{\sqrt{3x + 10 - x^2}} + \frac{1}{\sqrt{x + |x|}} \) is \( (a, b) \), then \( (1 + a)^2 + b^2 \) is equal to:
- JEE Main - 2025
- Functions
- Let \( A \) be a \( 3 \times 3 \) matrix such that \( X^T AX = 0 \) for all nonzero \( 3 \times 1 \) matrices \( X = \begin{pmatrix} x \\ y \\ z \end{pmatrix} \). \[ A = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}, \quad A = \begin{bmatrix} 1 \\ 4 \\ -5 \end{bmatrix}, \quad A = \begin{bmatrix} 1 \\ 2 \\ 1 \end{bmatrix}, \quad A = \begin{bmatrix} 0 \\ 4 \\ -8 \end{bmatrix} \] If \( \det(\text{adj}(2(A + I))) = 2^{\alpha} 3^{\beta} 5^{\gamma} \), \( \alpha, \beta, \gamma \in \mathbb{N} \), then \( \alpha^2 + \beta^2 + \gamma^2 \) is:
In the given circuit the sliding contact is pulled outwards such that the electric current in the circuit changes at the rate of 8 A/s. At an instant when R is 12 Ω, the value of the current in the circuit will be A.- JEE Main - 2025
- Electrical Circuits
- Let \( f: [0, 3] \to A \) be defined by \( f(x) = 2x^3 - 15x^2 + 36x + 7 \) and \( g: [0, \infty) \to B \) be defined by \( g(x) = \frac{x}{x^{2025} + 1}. \) If both functions are onto and \( S = \{ x \in \mathbb{Z} : x \in A { or } x \in B \} \), then \( n(S) \) is equal to:
- JEE Main - 2025
- Functions
Let A be a 3 × 3 matrix such that \(\text{det}(A) = 5\). If \(\text{det}(3 \, \text{adj}(2A)) = 2^{\alpha \cdot 3^{\beta} \cdot 5^{\gamma}}\), then \( (\alpha + \beta + \gamma) \) is equal to:
- JEE Main - 2025
- Matrix Operations
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
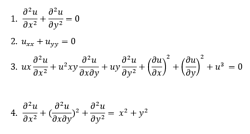
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
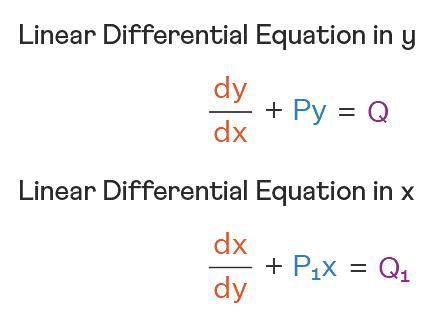
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations