Standing waves are produced in $10\, m$ long stretched string. If the string vibrates in $5$ segments and wave velocity is $20\,m/s$, its frequency is
- 5 Hz
- 4 Hz
- 2 Hz
- 10 Hz
The Correct Option is A
Solution and Explanation
$\therefore 5 \frac{\lambda}{2}=10$
$\Rightarrow \lambda=4\, m$
Given, the velocity of the wave $v=20\, m / s$
$\therefore$ Frequency $v=\frac{v}{\lambda}=\frac{20}{4}=5\, s ^{-1}=5\, Hz$
Top Questions on doppler effect
- When both the source of sound and observer approach each other with a speed equal to 10% of the speed of sound, then the percentage change in frequency heard by the observer is nearly
- AP EAPCET - 2025
- Physics
- doppler effect
- A passenger is sitting in a fast moving train. The engine of the train blows a whistle of frequency N. If the apparent frequency of sound heard by the passengers is \( N' \), then:
- MHT CET - 2025
- Physics
- doppler effect
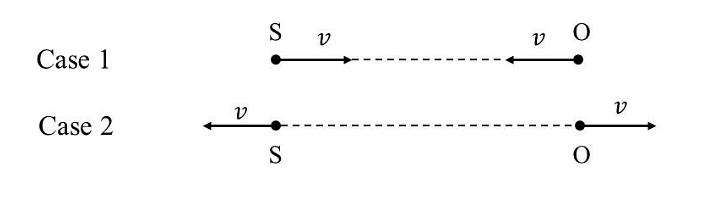
- A source (S) of sound has frequency\( 240 Hz\). When the observer (O) and the source move towards each other at a speed \(v\) with respect to the ground (as shown in Case 1 in the figure), the observer measures the frequency of the sound to be \(288 Hz\). However, when the observer and the source move away from each other at the same speed v with respect to the ground (as shown in Case 2 in the figure), the observer measures the frequency of sound to be \(n\) Hz. The value of \(n\) is _____.
- JEE Advanced - 2024
- Physics
- doppler effect
- A galaxy is moving away from the Earth so that a spectral line at 6000 Å is observed at 6300 Å. Then the speed of the galaxy with respect to the Earth is
- KCET - 2024
- Physics
- doppler effect
- A train is moving with a speed of \(10 m/s\) towards a platform and blows a horn with frequency \(400 Hz\). Find the frequency heard by a passenger standing on the platform. Take speed of sound = \(310 m/s\).
- JEE Main - 2023
- Physics
- doppler effect
Questions Asked in NEET exam
- A photon and an electron (mass \(m\)) have the same energy \(E\). The ratio \( \frac{\lambda_{\text{photon}}}{\lambda_{\text{electron}}} \) of their de Broglie wavelengths is: (\(c\) is the speed of light)
- NEET (UG) - 2025
- Dual nature of radiation and matter
A bob of heavy mass \(m\) is suspended by a light string of length \(l\). The bob is given a horizontal velocity \(v_0\) as shown in figure. If the string gets slack at some point P making an angle \( \theta \) from the horizontal, the ratio of the speed \(v\) of the bob at point P to its initial speed \(v_0\) is :
- NEET (UG) - 2025
- Pendulums
- De-Broglie wavelength of an electron orbiting in the \(n = 2\) state of hydrogen atom is close to (Given Bohr radius = 0.052 nm):
- NEET (UG) - 2025
- de broglie hypothesis
- The plates of a parallel plate capacitor are separated by d. Two slabs of different dielectric constant \(K_1\) and \(K_2\) with thickness \(d/2\) and \(d/2\) respectively are inserted in the capacitor. Due to this, the capacitance becomes two times larger than when there is nothing between the plates. If \(K_1 = 1.25 K_2\), the value of \(K_2\) is :
- NEET (UG) - 2025
- Capacitors and Capacitance
- A wire of resistance \(R\) is cut into 8 equal pieces. From these pieces, two equivalent resistances are made by adding four of these together in parallel. Then these two are added in series. The net effective resistance of the combination is:
- NEET (UG) - 2025
- Resistance
Concepts Used:
Doppler Effect
The Doppler effect is a phenomenon caused by a moving wave source that causes an apparent upward shift in frequency for observers who are approaching the source and a visible downward change in frequency for observers who are retreating from the source. It's crucial to note that the impact isn't caused by a change in the source's frequency.
The Doppler effect may be seen in any wave type, including water waves, sound waves, and light waves. We are most familiar with the Doppler effect because of our encounters with sound waves