Let x be an $n \times 1$ matrix. Let O and I be the zero, and identity matrices of order n, respectively. Define $P = - \frac{xx^T}{x^Tx}$ is the transpose of x.
Then which of the following options is always CORRECT?
- $P^2 - P = O$
- $P^2 - P = I$
- $P^2 + P = O$
- $P^2 + P = I$
The Correct Option is C
Solution and Explanation
Since it is given that
\(P= - \frac{x x^{T}}{x^{T} x}\)
\(\Rightarrow x^{T} xP = -xx^{T}\)
On applying transpose both sides, we get
\(P^{T}x^{T}x = -x^{T}x\)
\(\Rightarrow \left(P^{T} +I\right) x^{T}x = O\)
\(\Rightarrow P^{T} + I =0\)
\(\Rightarrow P^T = -I \therefore P = -I \left\{ \because I^{T} = I\right\}\)
so \(P^{2} +P = I - I =O\)
\(\Rightarrow P^{2} +P = O\)
Therefore, The Correct Answer is (C) P2 + P = O
Top Questions on Transpose of a Matrix
- Let P be a square matrix such that P2 = I – P. For α, β, γ, δ ∈ N, if Pα + Pβ = γI – 29P and Pα – Pβ = δI – 13P, then α + β + γ – δ is equal to
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
- Let B =\(\begin{bmatrix} 1 & 3 & α \\ 1 & 2& 3 \\ α & α & 4 \end{bmatrix}\) , α>2 be the adjoint of a matrix A and |A| = 2, then [α - 2α α] B\(\begin{bmatrix} α \\ -2α \\ α \end{bmatrix}\)is equal to
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
- Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A : For matrix A =\(\begin{bmatrix} 1 & 2 \\ 8 & 16 \end{bmatrix}\),rank of A = r(A) = 1
Reason R: For matrix A if |A| = 0, then it implies that rank of matrix A given by r(A) is less than full rank.
In the light of the above statements, choose the most appropriate answer from the options given below:- CUET (PG) - 2023
- Mathematics
- Transpose of a Matrix
- if A=\(\frac{1}{5! 6! 7!}\begin{bmatrix} 5! & 6! & 7!\\ 6! & 7! & 8! \\ 7! & 8! & 9! \end{bmatrix}\), then |adj(adj(2A))| is equal t
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
- Let Dk=\(\begin{vmatrix} 1 & 2k & 2k-1\\ n & n^2+n+2 & n^2 \\ n & n^2+n & n^2+n+2 \end{vmatrix} \) If \(∑^n_{k=1} D_k=96,\) The n is equal to
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
Questions Asked in UPSEE exam
- A carnot engine takes 300 calories of heat at 500 K and rejects 150 calories of heat to the sink. The temperature of the sink is
- UPSEE - 2019
- Heat Transfer
- Which of the following is not permissible arrangement of electrons in an atom.
- UPSEE - 2019
- Quantum Mechanical Model of Atom
- If det $\begin{bmatrix}1&1&2\\ 2&4&9\\ t&t^{2}&1+t^{3}\end{bmatrix} = 0 $ , then the values of t are
- UPSEE - 2019
- Properties of Determinants
- The imaginary part of $\left( \frac{1}{2} + \frac{1}{2}i\right)^{10} $ is
- UPSEE - 2019
- Complex Numbers and Quadratic Equations
- Let S be the set of all right angled triangles with integer sides forming consecutive terms of an arithmetic progression. The number of triangles in S with perimeter less than 30 is
- UPSEE - 2019
- Arithmetic Progression
Concepts Used:
Transpose of a Matrix
The matrix acquired by interchanging the rows and columns of the parent matrix is called the Transpose matrix. The transpose matrix is also defined as - “A Matrix which is formed by transposing all the rows of a given matrix into columns and vice-versa.”
The transpose matrix of A is represented by A’. It can be better understood by the given example:
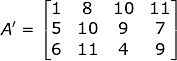
Now, in Matrix A, the number of rows was 4 and the number of columns was 3 but, on taking the transpose of A we acquired A’ having 3 rows and 4 columns. Consequently, the vertical Matrix gets converted into Horizontal Matrix.
Hence, we can say if the matrix before transposing was a vertical matrix, it will be transposed to a horizontal matrix and vice-versa.
Read More: Transpose of a Matrix