Let the plane ax + by + cz = d pass through (2, 3, –5) and is perpendicular to the planes 2x + y – 5z = 10 and 3x + 5y – 7z = 12. If a, b, c, d are integers d > 0 and gcd (|a|, |b|, |c|, d) = 1, then the value of a + 7b + c + 20d is equal to :
18
20
24
22
The Correct Option is D
Solution and Explanation
The correct answer is (D) : 22
Equation of plane through point (2, 3, –5) and perpendicular to planes 2x + y – 5z = 10 and 3x + 5y – 7z = 12 is
\(\begin{vmatrix} x-2 & y-3 & z+5 \\ 2 & 1 & -5 \\ 3 & 5 & -7 \\ \end{vmatrix} = 0\)
∴ Equation of plane is (x – 2) (– 7 + 25) – (y – 3) (– 14 + 15) + (z + 5) · 7 = 0
∴ 18x – y + 7z + 2 = 0
⇒ 18x – y + 7z = – 2
∴ – 18x + y – 7z = 2
On comparing with ax + by + cz = d where d > 0 is
a = – 18, b = 1, c = – 7, d = 2
Therefore a + 7b + c + 20d = 22
Top Questions on Three Dimensional Geometry
Show that the following lines intersect. Also, find their point of intersection:
Line 1: \[ \frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4} \]
Line 2: \[ \frac{x - 4}{5} = \frac{y - 1}{2} = z \]
- CBSE CLASS XII - 2025
- CBSE Compartment XII - 2025
- Mathematics
- Three Dimensional Geometry
The vector equations of two lines are given as:
Line 1: \[ \vec{r}_1 = \hat{i} + 2\hat{j} - 4\hat{k} + \lambda(4\hat{i} + 6\hat{j} + 12\hat{k}) \]
Line 2: \[ \vec{r}_2 = 3\hat{i} + 3\hat{j} - 5\hat{k} + \mu(6\hat{i} + 9\hat{j} + 18\hat{k}) \]
Determine whether the lines are parallel, intersecting, skew, or coincident. If they are not coincident, find the shortest distance between them.
- CBSE CLASS XII - 2025
- CBSE Compartment XII - 2025
- Mathematics
- Three Dimensional Geometry
Determine the vector equation of the line that passes through the point \( (1, 2, -3) \) and is perpendicular to both of the following lines:
\[ \frac{x - 8}{3} = \frac{y + 16}{7} = \frac{z - 10}{-16} \quad \text{and} \quad \frac{x - 15}{3} = \frac{y - 29}{-8} = \frac{z - 5}{-5} \]
- CBSE CLASS XII - 2025
- CBSE Compartment XII - 2025
- Mathematics
- Three Dimensional Geometry
- Find the value of λ, if the points A(−1,−1,2), B(2,8,λ), C(3,11,6) are collinear.
- CBSE CLASS XII - 2025
- CBSE Compartment XII - 2025
- Mathematics
- Three Dimensional Geometry
- Find the length of the diagonal of a rectangle with length 6 cm and breadth 8 cm.
- MHT CET - 2025
- Mathematics
- Three Dimensional Geometry
Questions Asked in JEE Main exam
- If \( \alpha + i\beta \) and \( \gamma + i\delta \) are the roots of the equation \( x^2 - (3-2i)x - (2i-2) = 0 \), \( i = \sqrt{-1} \), then \( \alpha\gamma + \beta\delta \) is equal to:
- JEE Main - 2025
- Complex numbers
- A galvanometer having a coil of resistance 30 \( \Omega \) needs 20 mA of current for full-scale deflection. If a maximum current of 3 A is to be measured using this galvanometer, the resistance of the shunt to be added to the galvanometer should be \( X \, \Omega \), where \( X \) is:
- JEE Main - 2025
- Electrical Circuits and Shunt Resistance
- The variance of the numbers 8, 21, 34, 47, \dots, 320, is:
- JEE Main - 2025
- Arithmetic Progression and Variance
- Given below are two statements: one is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : If Young’s double slit experiment is performed in an optically denser medium than air, then the consecutive fringes come closer.
Reason (R) : The speed of light reduces in an optically denser medium than air while its frequency does not change.
In the light of the above statements, choose the most appropriate answer from the options given below : - The increase in pressure required to decrease the volume of a water sample by 0.2percentage is \( P \times 10^5 \, \text{Nm}^{-2} \). Bulk modulus of water is \( 2.15 \times 10^9 \, \text{Nm}^{-2} \). The value of \( P \) is ________________.
- JEE Main - 2025
- System of Particles & Rotational Motion
Concepts Used:
Three Dimensional Geometry
Mathematically, Geometry is one of the most important topics. The concepts of Geometry are derived w.r.t. the planes. So, Geometry is divided into three major categories based on its dimensions which are one-dimensional geometry, two-dimensional geometry, and three-dimensional geometry.
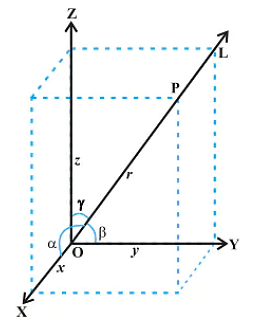
Direction Cosines and Direction Ratios of Line:
Consider a line L that is passing through the three-dimensional plane. Now, x,y and z are the axes of the plane and α,β, and γ are the three angles the line makes with these axes. These are commonly known as the direction angles of the plane. So, appropriately, we can say that cosα, cosβ, and cosγ are the direction cosines of the given line L.
