Let S be the sample space of all five digit numbers. It p is the probability that a randomly selected number from S, is multiple of 7 but not divisible by 5, then 9p is equal to
Let S be the sample space of all five digit numbers. It p is the probability that a randomly selected number from S, is multiple of 7 but not divisible by 5, then 9p is equal to
- 1.0146
- 1.2085
- 1.0285
- 1.1521
The Correct Option is C
Solution and Explanation
The correct answer is (C):
Among the 5 digit numbers,
First number divisible by 7 is 10003 and last is 99995.
⇒ Number of numbers divisible by 7.
= \(\frac{99995-10003}{7} + 1\)
= 12875
First number divisible by 35 is 10010 and last is 99995.
⇒ Number of numbers divisible by 35 =\(\frac{ 99995-10010}{35}+1 = 2572\)
Hence number of number divisible by 7 but not by 5
= 12857 – 2572
= 10285
9P =\( \frac{10285}{90000} × 9\)
= 1.0285
Top Questions on types of differential equations
- If \( m_1 \) and \( m_2 \) are the slopes of the direct common tangents drawn to the circles \[ x^2 + y^2 - 2x - 8y + 8 = 0 \quad \text{and} \quad x^2 + y^2 - 8x + 15 = 0 \] then \( m_1 + m_2 \) is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- If \( (2,3) \) is the focus and \( x - y + 3 = 0 \) is the directrix of a parabola, then the equation of the tangent drawn at the vertex of the parabola is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- If the focus of an ellipse is \((-1,-1)\), equation of its directrix corresponding to this focus is \(x + y + 1 = 0\) and its eccentricity is \(\frac{1}{\sqrt{2}}\), then the length of its major axis is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- The equation of the common tangent to the parabola \(y^2 = 8x\) and the circle \(x^2 + y^2 = 2\) is \(ax + by + 2 = 0\). If \(-\frac{a}{b}>0\), then \(3a^2 + 2b + 1 =\)
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- The axis of a parabola is parallel to Y-axis. If this parabola passes through the points \( (1,0), (0,2), (-1,-1) \) and its equation is \( ax^2 + bx + cy + d = 0 \), then \( \frac{ad}{bc} \) is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
Questions Asked in JEE Main exam
In the given circuit the sliding contact is pulled outwards such that the electric current in the circuit changes at the rate of 8 A/s. At an instant when R is 12 Ω, the value of the current in the circuit will be A.- JEE Main - 2025
- Electrical Circuits
- Let \( \vec{a} = \hat{i} + 2\hat{j} + \hat{k} \) and \( \vec{b} = 2\hat{i} + 7\hat{j} + 3\hat{k} \). Let \( L_1 : \vec{r} = (-\hat{i} + 2\hat{j} + \hat{k}) + \lambda \vec{a}, \lambda \in {R} \) and \( L_2 : \vec{r} = (\hat{j} + \hat{k}) + \mu \vec{b}, \mu \in \mathbb{R} \) be two lines. If the line \( L_3 \) passes through the point of intersection of \( L_1 \) and \( L_2 \), and is parallel to \( \vec{a} + \vec{b} \), then \( L_3 \) passes through the point:
- JEE Main - 2025
- Vectors
Let $ P_n = \alpha^n + \beta^n $, $ n \in \mathbb{N} $. If $ P_{10} = 123,\ P_9 = 76,\ P_8 = 47 $ and $ P_1 = 1 $, then the quadratic equation having roots $ \alpha $ and $ \frac{1}{\beta} $ is:
- JEE Main - 2025
- Relations and functions
For $ \alpha, \beta, \gamma \in \mathbb{R} $, if $$ \lim_{x \to 0} \frac{x^2 \sin \alpha x + (\gamma - 1)e^{x^2} - 3}{\sin 2x - \beta x} = 3, $$ then $ \beta + \gamma - \alpha $ is equal to:
The maximum speed of a boat in still water is 27 km/h. Now this boat is moving downstream in a river flowing at 9 km/h. A man in the boat throws a ball vertically upwards with speed of 10 m/s. Range of the ball as observed by an observer at rest on the river bank is _________ cm. (Take \( g = 10 \, {m/s}^2 \)).
- JEE Main - 2025
- System of Particles & Rotational Motion
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
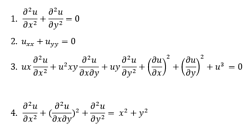
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
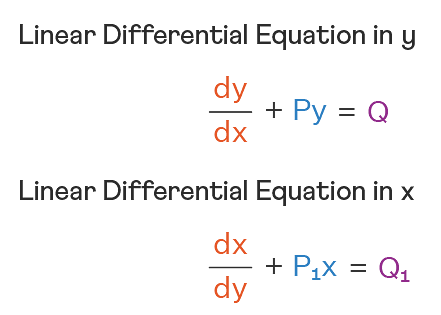
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations