Let \( S \) be a set consisting of 10 elements.
The number of tuples of the form \( (A, B) \) such that \( A \) and \( B \) are subsets of \( S \), and \( A \subseteq B \), is \(\underline{\hspace{2cm}}\).
The number of tuples of the form \( (A, B) \) such that \( A \) and \( B \) are subsets of \( S \), and \( A \subseteq B \), is \(\underline{\hspace{2cm}}\).
Show Hint
Correct Answer: 59049
Solution and Explanation
- The element is not in \( B \)
- The element is in \( B \) but not in \( A \)
- The element is in both \( A \) and \( B \)
Since \( A \subseteq B \), an element cannot be in \( A \) without being in \( B \).
Thus, each element has exactly 3 independent choices.
Therefore, the total number of such ordered pairs \( (A, B) \) is: \[ 3^{10} = 59049 \] Final Answer: \[ \boxed{59049} \]
Top Questions on Sets
- Mode of the data \( 19, 2, 6, 12, 12, 3, 5, 6, 18, 14, 6, 17, 2 \) is:
- The mean and mode of 5, 3, 9, 1, 9, 8, 9, 4 are m and n respectively, the value of m+n is?
- If A = {1, 2, {3, 4}, 5}, then which of the following is incorrect?
- If A and B are the two sets containing 3 and 6 elements respectively, then what can be the maximum number of elements in A∪B?
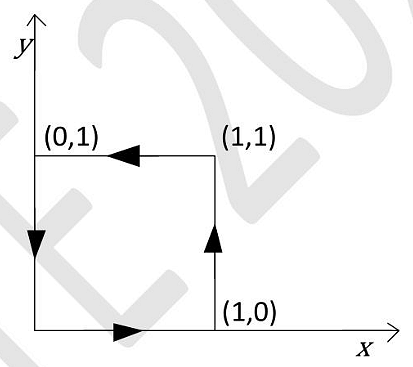
- For \(\vec{F}=(x+y)\hat{i}+(x+y)\hat{j}\) the value of \(\oint\vec{F}.d\vec{r}\) along the path shown in the figure is ________. Give your answer as an integer.
Questions Asked in GATE CS exam
In a 4-bit ripple counter, if the period of the waveform at the last flip-flop is 64 microseconds, then the frequency of the ripple counter in kHz is ______________. {(Answer in integer)}
- GATE CS - 2025
- Flip-Flop
Consider the following C code segment:
int x = 126, y = 105; do { if (x > y) x = x - y; else y = y - x; } while (x != y); printf("%d", x);The output of the given C code segment is ____________. (Answer in integer)
- GATE CS - 2025
- Programming in C
The following two signed 2’s complement numbers (multiplicand \( M \) and multiplier \( Q \)) are being multiplied using Booth’s algorithm:
Multiplicand (\( M \)) Multiplier (\( Q \)) 1100 1101 1110 1101 1010 0100 1010 1010 The total number of addition and subtraction operations to be performed is __________. (Answer in integer)
- GATE CS - 2025
- Complementation
The maximum value of \(x\) such that the edge between the nodes B and C is included in every minimum spanning tree of the given graph is __________ (answer in integer).

- GATE CS - 2025
- Programming and Data Structures
Consider the following C program

The value printed by the given C program is __________ (Answer in integer).- GATE CS - 2025
- Programming in C