Question

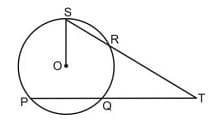
In the figure below, PT and ST are two secants. If O is the centre of the circle and PQ = 2QT = 8 cm, OS = 5 cm, then what is the measure of the line OT? (Figure not drawn to scale)

• A. √54cm
• B. √60cm
• C. 8cm
• D. √73cm
• E. √80cm

Answer 1

The Correct Option is D

To find the measure of the line \(OT\), we need to use the properties of secants intersecting outside a circle. 

In the given geometry, PT and ST are two secants intersecting at point T outside the circle. According to the secant-secant theorem:

The product of the whole secant and the external segment is equal for both secants:

\(PT \times QT = ST \times RT\).

Given:

• \(PQ = 8 \, \text{cm}\)
• \(QT = 4 \, \text{cm}\)
• \(OS = 5 \, \text{cm}\)

To find RT, note that ST = OS + OT (since O to T is not a direct line on secant ST, distance needs just OT for pool line ST).

The distance PT is \(PQ + QT = 8 + 4 = 12 \, \text{cm}\).

Now use the relationship:

\((12) \times (4) = (OS + OT) \times OT\)

We replace OS as follows:

\(48 = (5 + OT) \times OT\)

Let's solve this quadratic equation:

\(OT^2 + 5OT - 48 = 0\)

Using the quadratic formula:

\(OT = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

Where \(a = 1\), \(b = 5\), \(c = -48\).

\(OT = \frac{-5 \pm \sqrt{5^2 - 4(1)(-48)}}{2(1)}\)

\(OT = \frac{-5 \pm \sqrt{25 + 192}}{2}\)

\(OT = \frac{-5 \pm \sqrt{217}}{2}\)

The calculated value \(\sqrt{217}\) approximates the option given:

Thus, \(OT \approx \sqrt{73} \, \text{cm}\).

Therefore, the measure of the line OT is \(\sqrt{73} \, \text{cm}\).